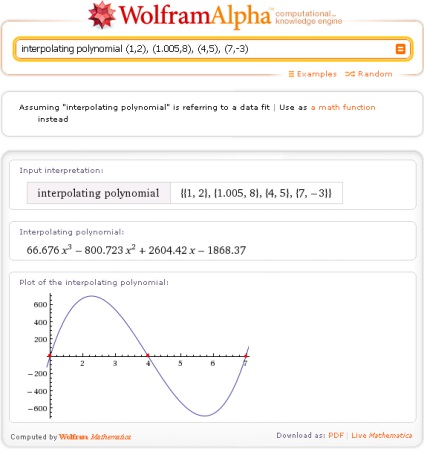
Interpolarea este un fel de aproximare. Cu toate acestea, spre deosebire de apropiere prin metoda celor mai mici pătrate, care dă ecuația funcției cu graficul care se extinde la o distanță minimă de la fiecare dintre aceste puncte, sarcina interpolare este de a găsi ecuația funcției, graficul care trece exact prin toate punctele indicate.
Există diferite tipuri de interpolare. Wolfram | Alpha folosește interpolarea polinomială și o execută la polinom interpolând la cerere
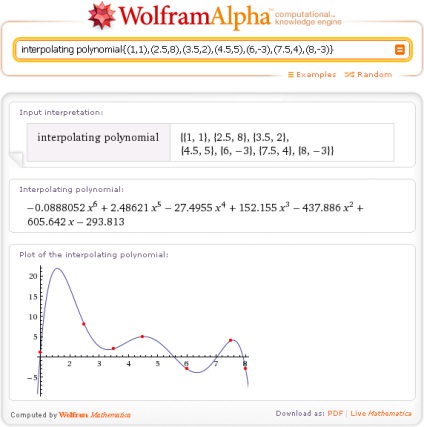
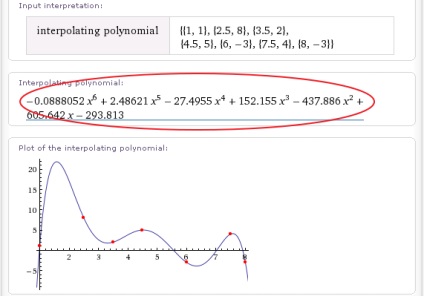
Ca răspuns, Wolfram | Alpha va da (b) un set de informații despre această expresie, de parcă ați fi introdus manual:
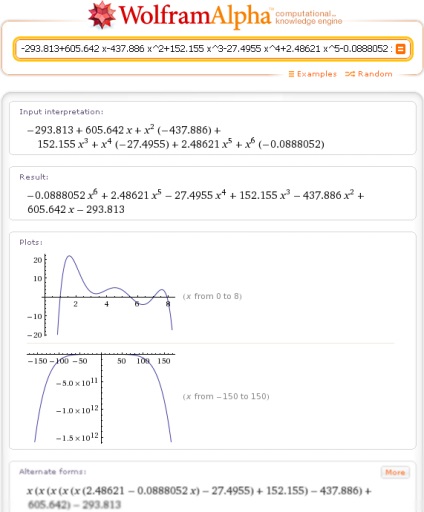
În cele din urmă, (c) pentru a calcula valoarea polinomului de interpolare, la un moment dat (x = 4), trebuie doar să specificați Wolfram fereastra de interogare | Alpha, după valoarea separate prin virgulă polinomială a intrat de argument pentru a obține acest lucru:

Aproximarea aceluiași set de puncte, atunci când nici tipul, nici ordinea modelului de aproximare nu sunt specificate, dau următoarele:
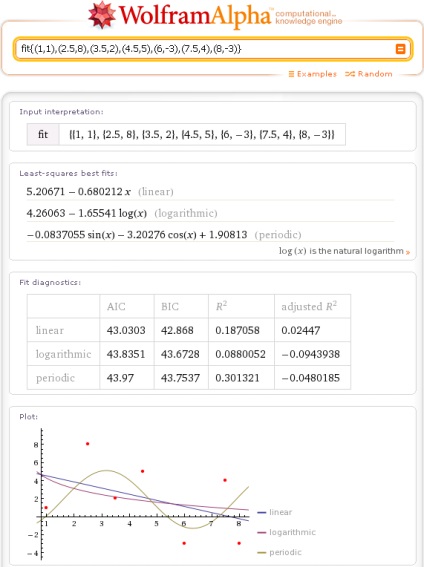
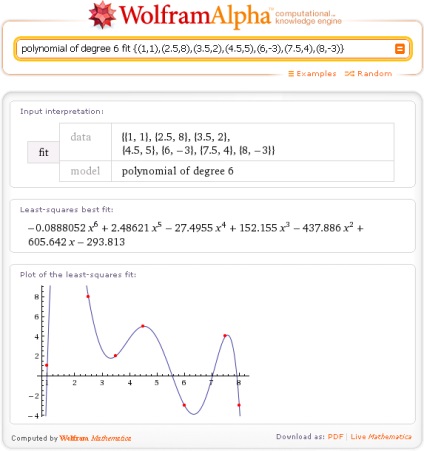
Se poate obține un rezultat de aproximare care coincide cu rezultatul interpolării polinomiale. Pentru a face acest lucru, alegeți un model polinomial și specificați ordinea lui cu un număr mai mic decât numărul de puncte de date:
Pentru a efectua interpolarea, este important ca abscisele punctelor date să nu coincidă. De exemplu, aici este o astfel de cerere (este greșit!)
unde primul și al doilea punct au aceeași abscisă, dă rezultatul la prima vedere plauzibil, dar absolut greșit:
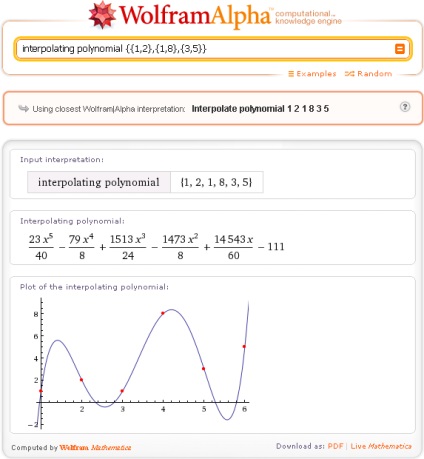
Aici, după cum puteți vedea, Wolfram | Alpha interpretează coordonatele a trei puncte de date ca o secvență de 6 numere - valorile funcției, iar ca abscise folosesc numerele membrilor acestei secvențe.
Dacă abscisele tuturor punctelor sunt cel puțin puțin diferite, atunci rezultatul este absolut corect (acesta este CORECT!):