Liniile drepte în spațiu pot fi paralele, intersectate sau traversate.
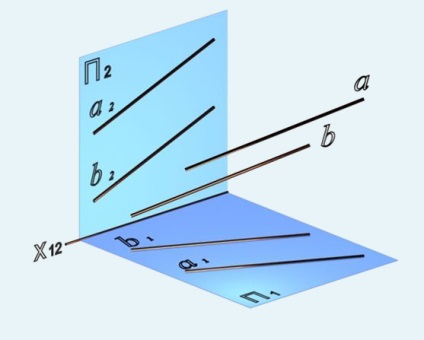
Fig. 24. Liniile paralele a și b
Dacă liniile sunt paralele (figurile 24, 25), atunci proiecțiile lor cu același nume sunt paralele: alubb (a1 ∥b1) = (a2 ∥b2)
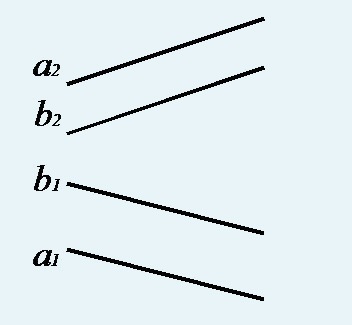
Fig. 25. Desenul complex al liniilor paralele a și b
Liniile intersectate au un punct comun (figurile 26, 27), adică punctele de intersecție ale proiecțiilor lor cu același nume se află pe linia comună:
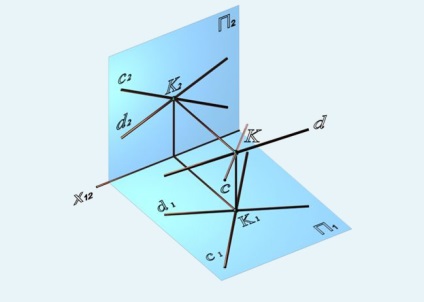
Fig. 26. Linii intersectate
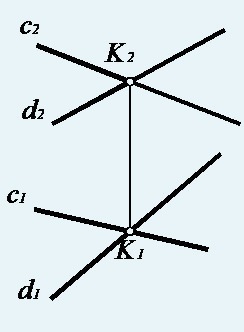
Fig. 27. Un desen complex al liniilor drepte intersectante c și d
Liniile drepte care nu au un punct comun și nu sunt paralele între ele sunt încrucișate (figurile 28, 29).
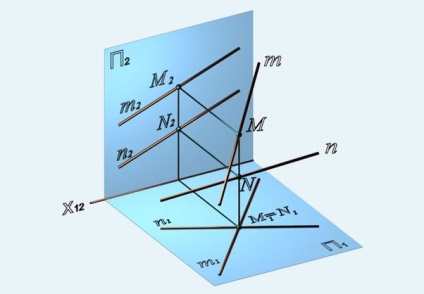
Fig. 28. Liniile drepte m și n
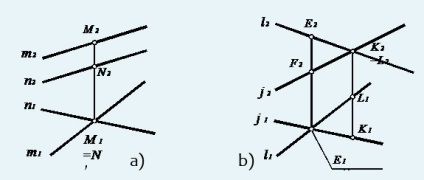
Fig. 29. Proiecțiile liniilor de trecere: a - liniile de trecere m și n; b sunt liniile intersectante l și j
Proiecțiile liniilor se intersectează, dar E1 K2 nu este o legătură comună (vezi figura 29, b).
Dacă liniile intersectate și paralele se află în același plan, liniile de traversare se află în două planuri paralele.