Cum funcționează acest lucru?
Să ne imaginăm o astfel de construcție.
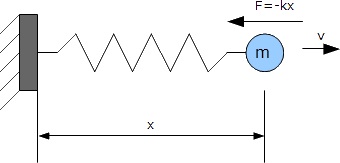
Greutățile atârnă la capătul arcului atașat la obiectul staționar. Dacă trageți ușor mingea la stânga sau la dreapta, va începe să oscileze cu o anumită perioadă T0. După cum știm din cursul fizic al școlii de la Google, această perioadă este egală cu:
Unde m este greutatea greutăților și k este rigiditatea arcului.
O frecvență corespunzătoare a vibrațiilor, respectiv, va fi 1 / T0. Cred că nu este un secret pentru cineva că dacă împingeți greutatea exact la această frecvență, amplitudinea oscilațiilor va fi maximă. Mai mult, cu cât împingerea este mai slabă, cu atât mai mare va fi amplitudinea oscilațiilor în funcție de frecvența împingerii.
Se dovedește un filtru mecanic. Să încercăm să-i facem modelul.
Din fizică, știm mai multe formule. Forța cu care arcul acționează asupra greutăților este egală cu:
unde k este rigiditatea arcului și x este tensiunea arcului. Această forță dă accelerația egală cu:
unde m este greutatea greutăților. De aici rezultă că:
Înlocuim k / m de T. Din prima formulă obținem că:
Acum la modelul în sine. Avem nevoie de 2 variabile - viteza greutății v și poziția greutății x. De asemenea, aveți nevoie de un pas de simulare t.
La fiecare pas viteza greutăților va varia în funcție de următoarea formulă:
și poziția prin formula
În sistemul nostru, t este în secunde, F este în hertz, iar x este în papagali. Este necesar să mergeți la milisecunde și kilogertsy, pentru a nu obține numere teribile. Toate formulele în acest mod magic rămân aceleași. )
punerea în aplicare
În primul rând, să încercăm să obținem procesul oscilatoriu.
Simulăm greutățile greutăților în trepte de 1/16 ms (înmulțirea cu 1/16 ms se înlocuiește cu deplasarea spre dreapta cu 4 biți). Datele sunt trimise la porturile B și D pentru a înțelege ce se întâmplă acolo. )
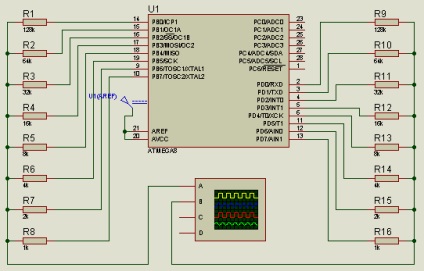
La porturi conectăm DAC-uri, și pentru ei un osciloscop.
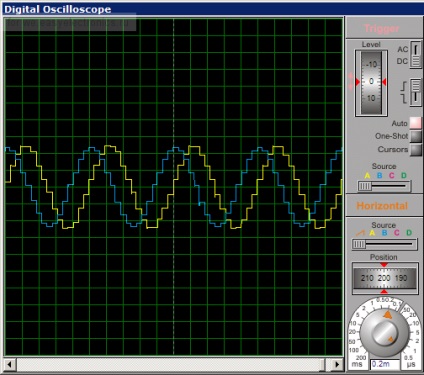
Se pare că funcționează. Poziția și viteza variază în cazul sinusoidelor deplasate cu 90 de grade, la fel ca curentul și tensiunea în circuitul oscilator. Frecventa este exact 1 kHz, asa cum a fost planificat. )
Acum adăugați semnalul de intrare.
Aici suntem un pic "împingător" cu mostre din ADC. Aici este conectat.
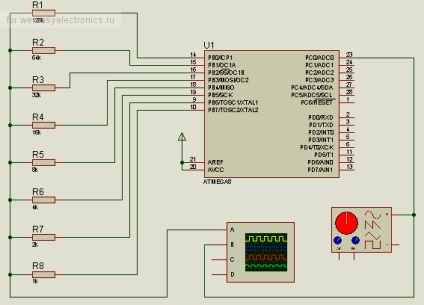
Iată rezultatul.
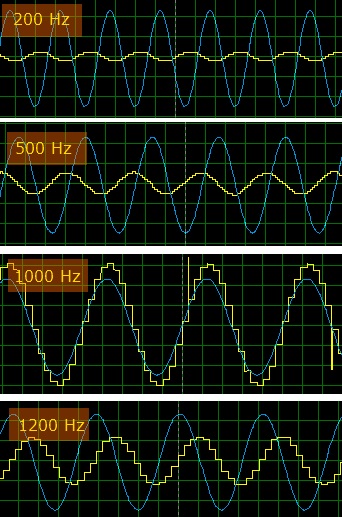
Graficul albastru - semnal de la generator, galben - de la DAC.
Am adunat această lumină intermitentă pentru a verifica ideea. )
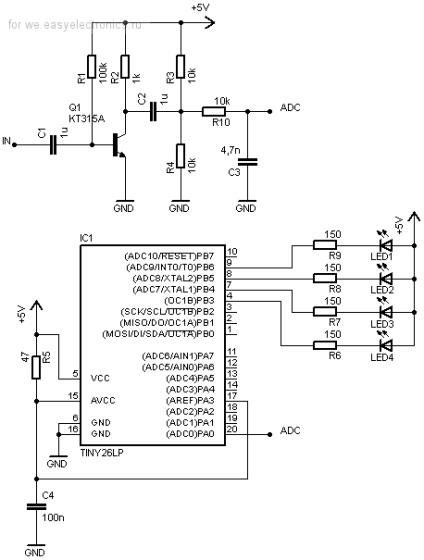
Iată codul final.
La colectorul de tranzistor ar trebui să fie aproximativ jumătate din puterea (dacă este ceva, este ajustat cu valoarea de R1). Tinka este pedepsită dintr-un lanț intern RC la 8 MHz.
Ei bine, asta e ...