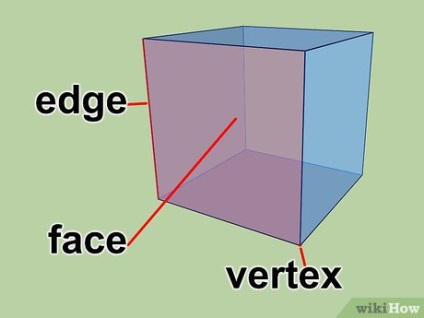

- Formula care descrie teorema lui Euler: F + V - E = 2
- F este numărul de fețe.
- V este numărul de vârfuri.
- E este numărul de margini.


- V = 2 - F + E
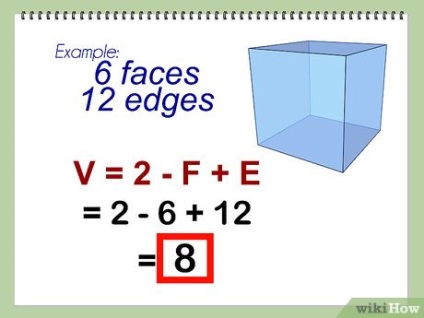

- Exemplu: găsiți numărul de vârfuri ale polyhedronului, care are 6 fețe și 12 margini.
- V = 2 - F + E
- V = 2 - 6 + 12
- V = -4 + 12
- V = 8
Metoda 2 din 5:
Căutați vârful regiunii unui sistem de inegalități liniare [2] Editați
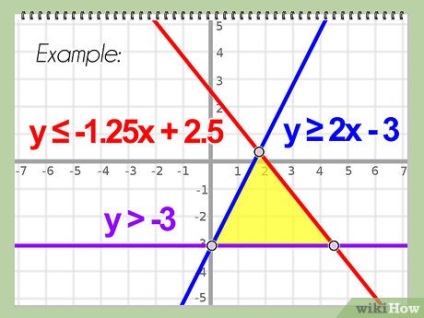

- Când utilizați un calculator de grafică, puteți să vă uitați la întregul grafic și să găsiți coordonatele nodurilor.


- Exemplu: având în vedere sistemul de inegalități:
- la <х
- y> - x + 4
- Conversia inegalităților în ecuații:
- y = x
- y = -x + 4
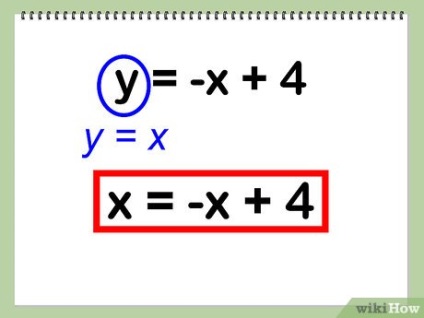
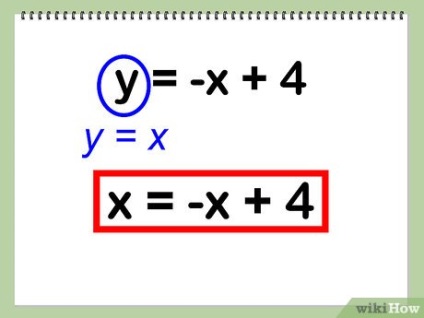
- exemplu:
- y = x
- y = -x + 4
- Substituim y = x în y = - x + 4:
- x = - x + 4
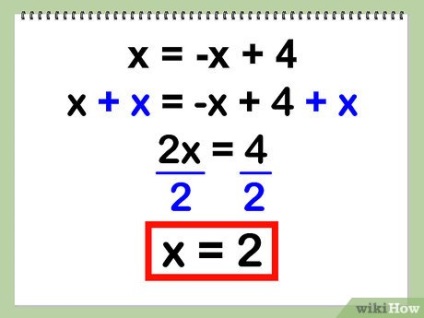
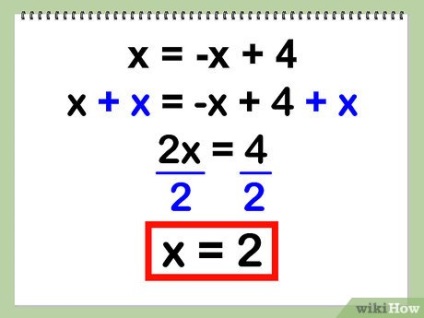
- Exemplu: x = - x + 4
- x + x = 4
- 2x = 4
- 2x / 2 = 4/2
- x = 2


- Exemplu: y = x
- y = 2
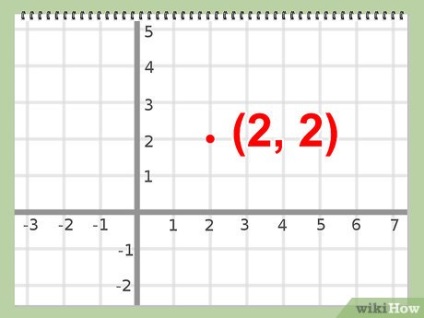

- Exemplu: vârful domeniului unui sistem dat de inegalități este punctul O (2,2).
Metoda 3 din 5:
Căutați vârful unei parabole prin axa de simetrie


- Exemplu: având în vedere ecuația patratică
- 3x2 - 6x - 45
- Mai întâi, puneți un factor comun în afara suportului: 3 (x2 - 2x - 15)
- Înmulțiți coeficienții "a" și "c": 1 * (-15) = -15.
- Găsiți două numere ale căror rezultate de multiplicare sunt -15, iar suma lor este egală cu coeficientul "b" (b = -2): 3 * (-5) = -15; 3 - 5 = -2.
- Înlocuiți valorile găsite în ecuația ax2 + kx + hx + c: 3 (x2 + 3x - 5x - 15).
- Extindeți ecuația inițială: f (x) = 3 * (x + 3) * (x - 5)


- Exemplu: 3 * (x + 3) * (x - 5) = 0
- x +3 = 0
- x = 5 = 0
- x = -3; x = 5
- Astfel, rădăcinile ecuației (sau punctul de intersecție cu axa X): A (-3, 0) și B (5, 0)
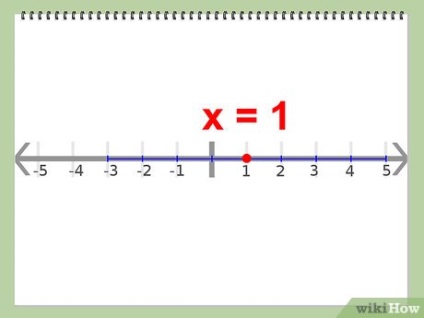

- Exemplu: x = 1; această valoare se situează în mijloc între -3 și +5.


- Exemplu: y = 3x2 - 6x - 45 = 3 (1) 2 - 6 (1) - 45 = -48
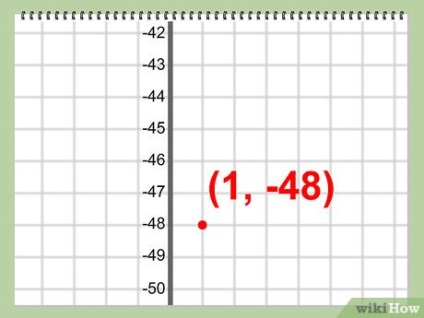

- Exemplu: vârful unei ecuații patrate date este punctul O (1, -48)