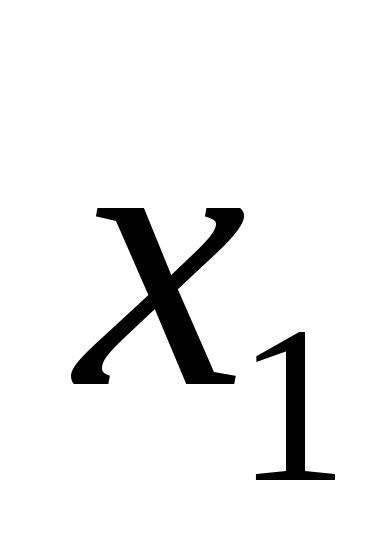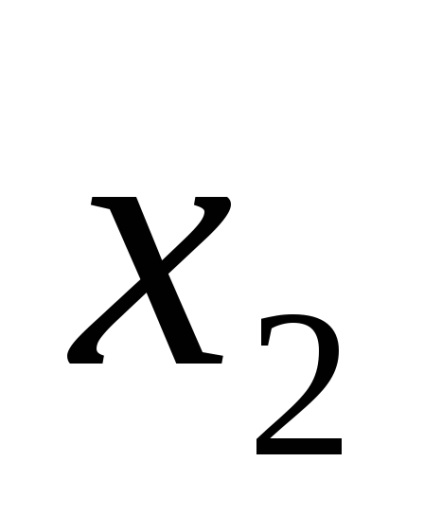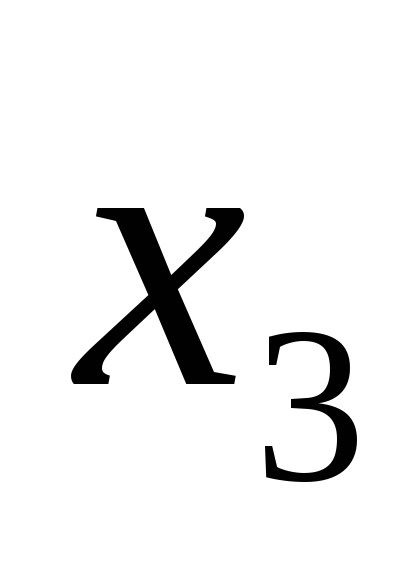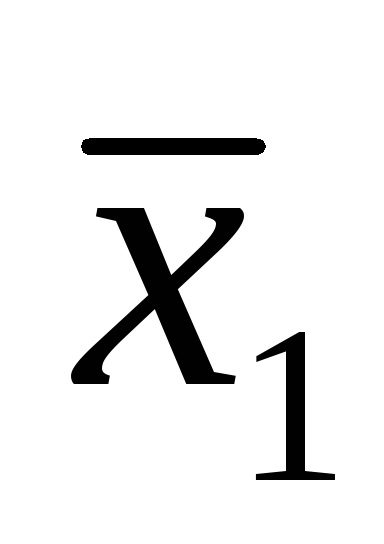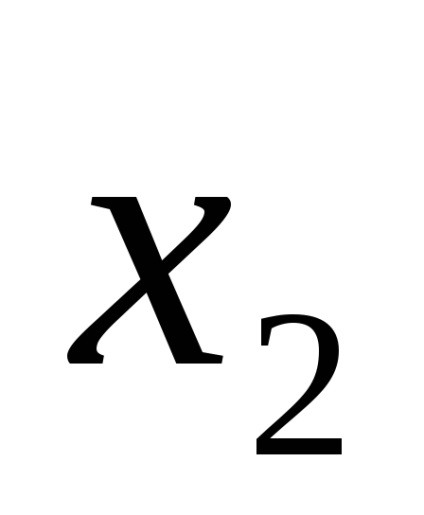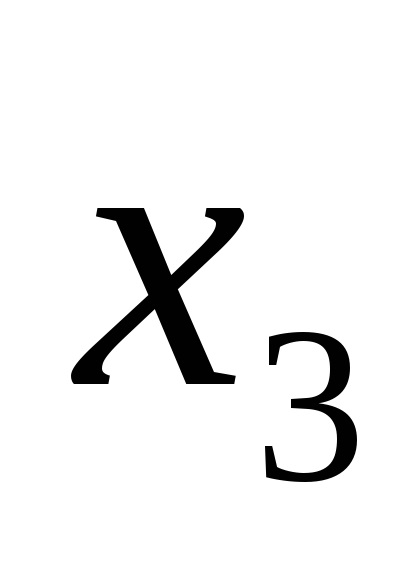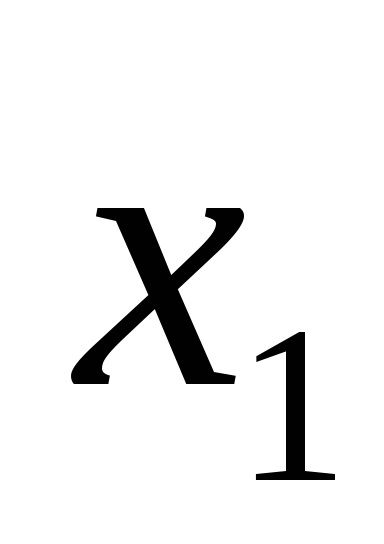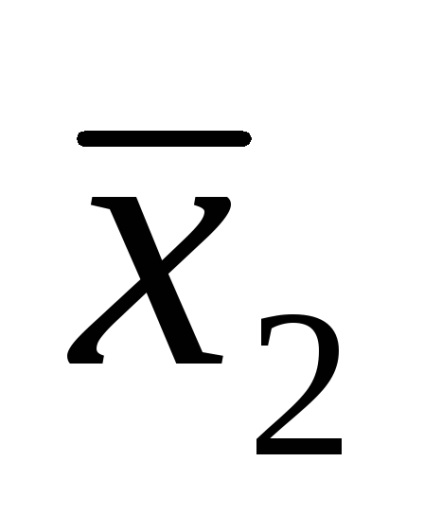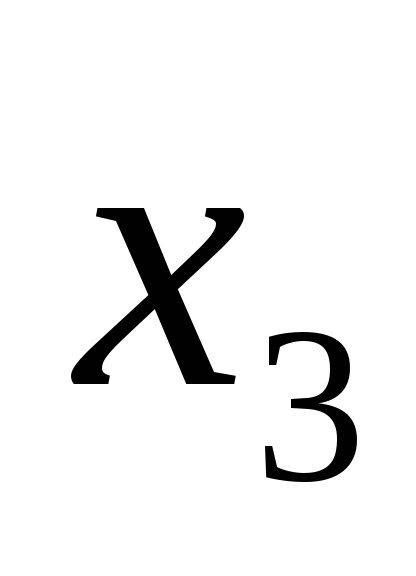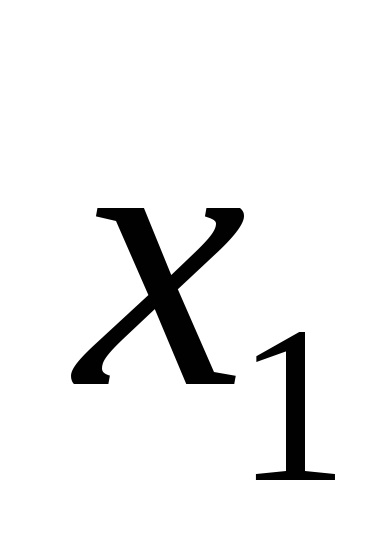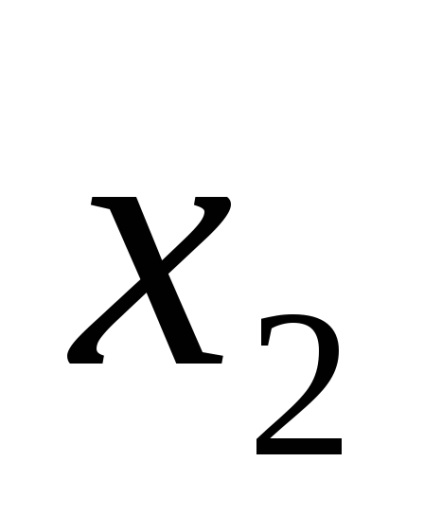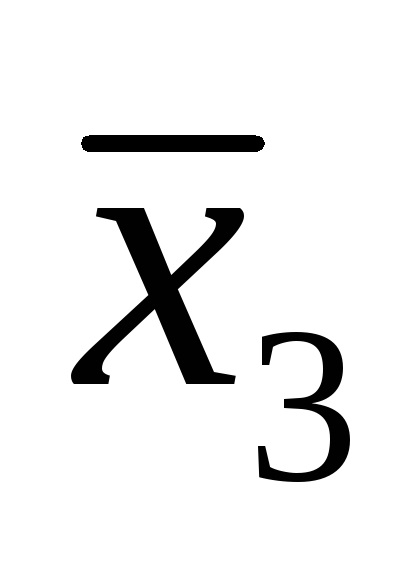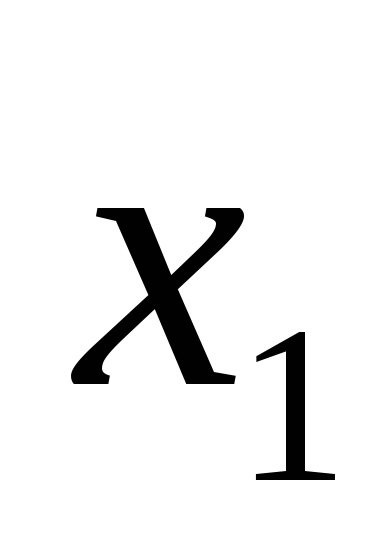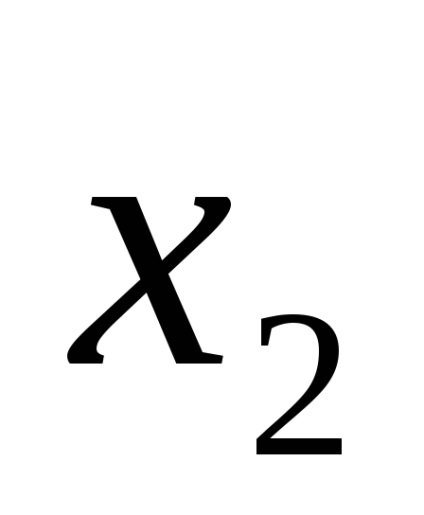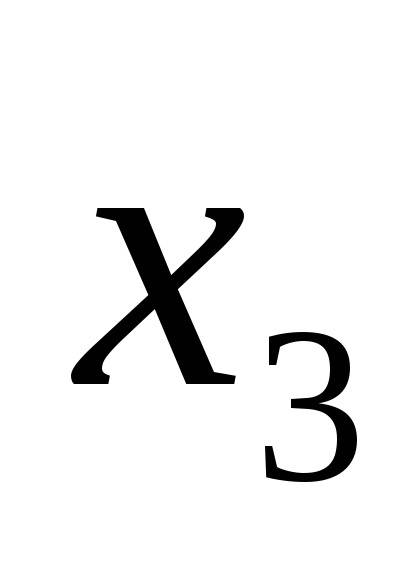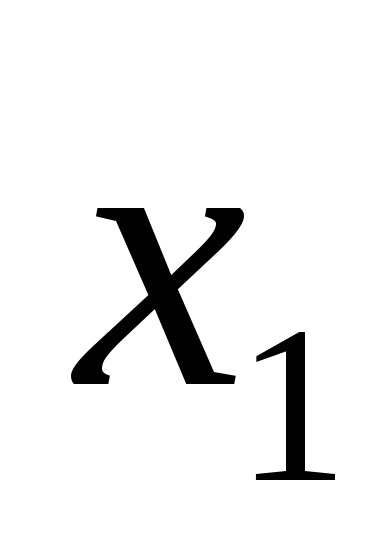Forme de funcții logice
Aceeași funcție logică poate fi scrisă în moduri diferite. De exemplu, funcția F (
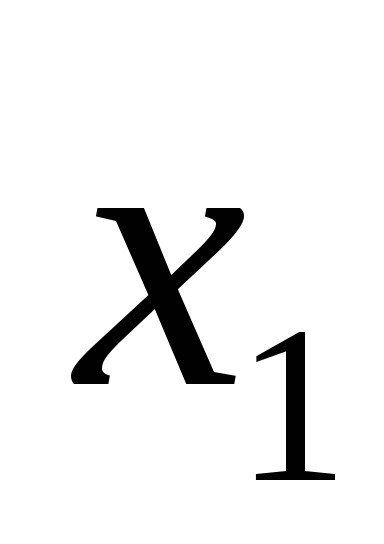
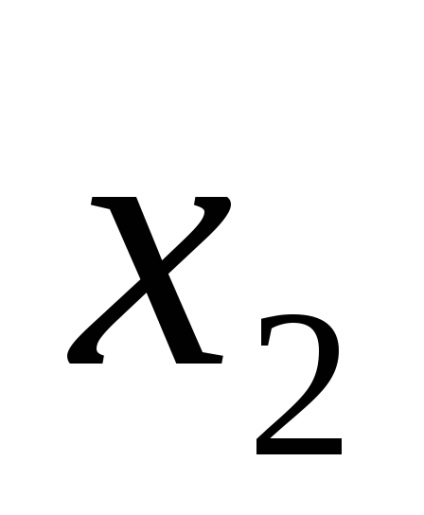
Este ușor să verificați echivalența expresiei prin înlocuirea valorilor din ele
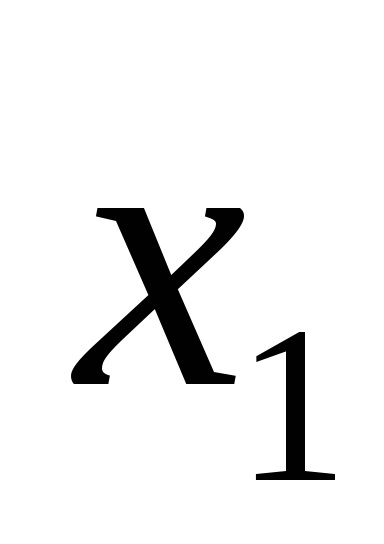
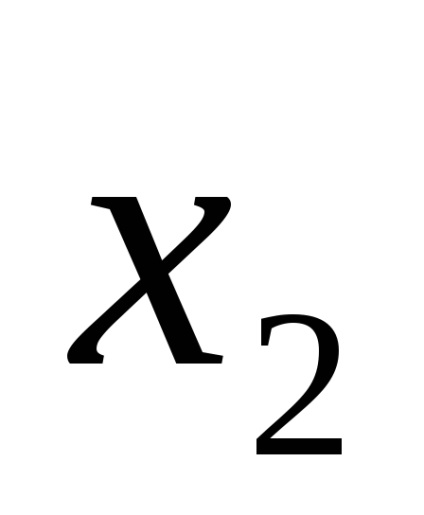
Elementar este o conjuncție, care include numai variabilele și negările lor.
Elementar este o disjuncție, care este o sumă logică a variabilelor și negările lor.
Conjuncțiile elementare (disjuncții) nu pot conține aceleași variabile, precum și variabilele cu negările lor. Astfel de disjuncții (conjuncții) trebuie transformate. În acest caz, acestea sunt simplificate și, de asemenea, se transformă în 0 sau 1.
Corectitudinea transformărilor poate fi verificată prin substituirea valorilor variabilelor. Combinarea elementară (disjuncția) poate fi caracterizată de un rang egal cu numărul de variabile din conjuncție (disjuncție). Conceptele conjuncțiilor și disjuncțiilor elementare fac posibilă definirea destul de simplă a unei forme disjunctive și conjunctive de înregistrare a funcțiilor logice.
O formă normală disjunctivă (DNF) este o formă în care o funcție logică este reprezentată ca o disjuncție a conjuncțiilor elementare, de exemplu: F =
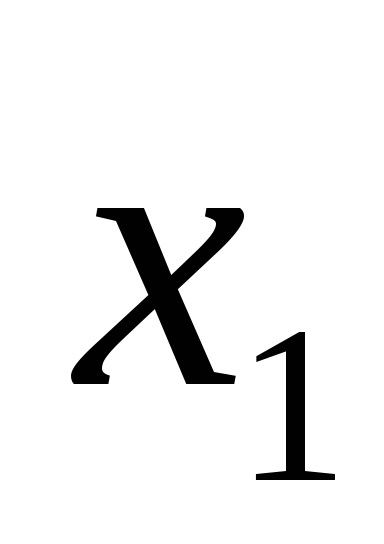
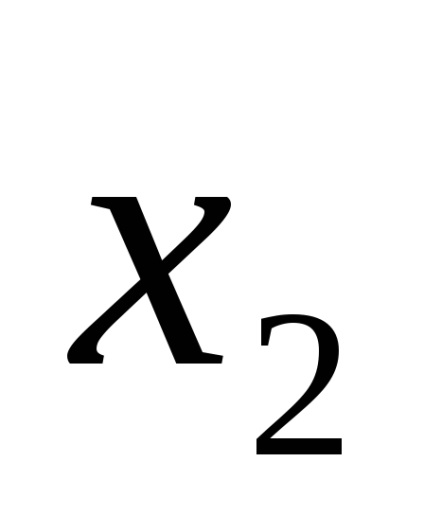
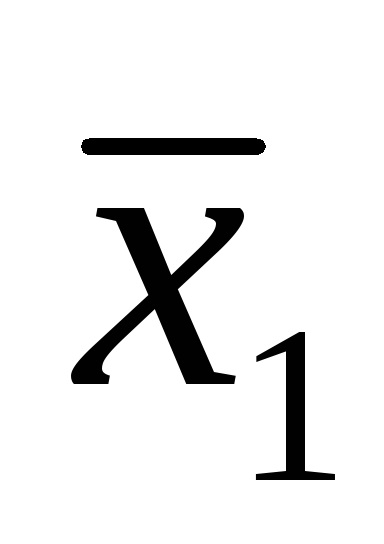
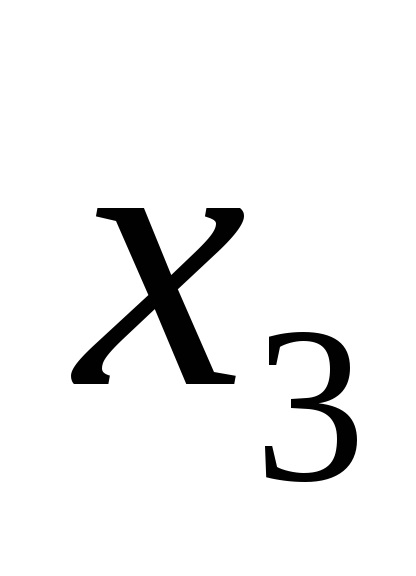
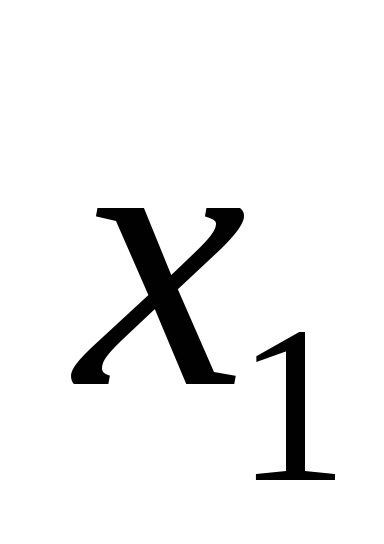
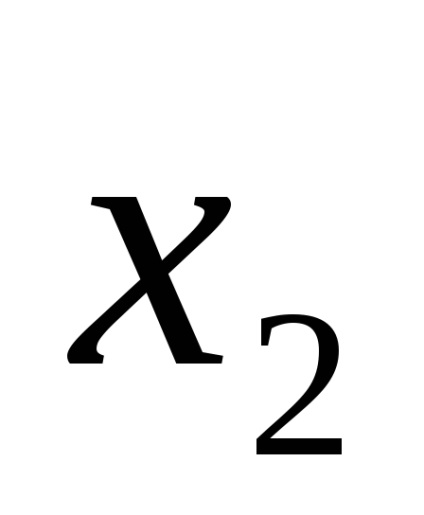
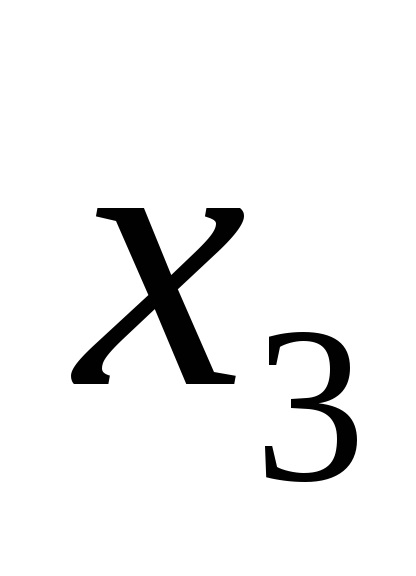
Funcțiile expresiilor (1) și (2) sunt, de asemenea, scrise în DNF.
O formă normală conjunctivă (CNF) este o formă în care funcția este reprezentată ca o conjuncție de disjuncții elementare, de exemplu: F = (
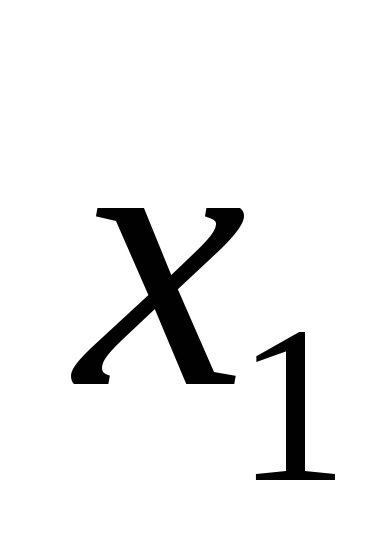
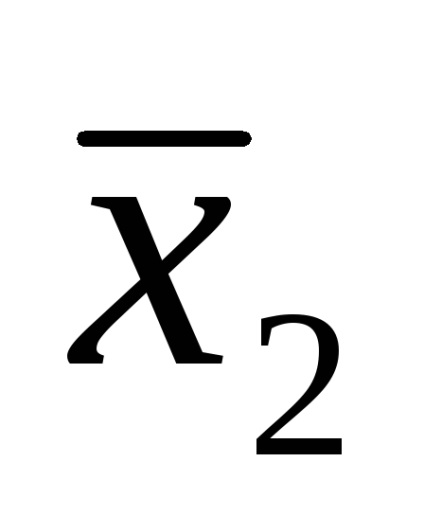
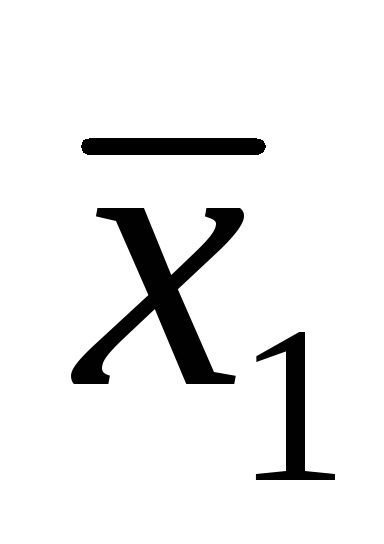
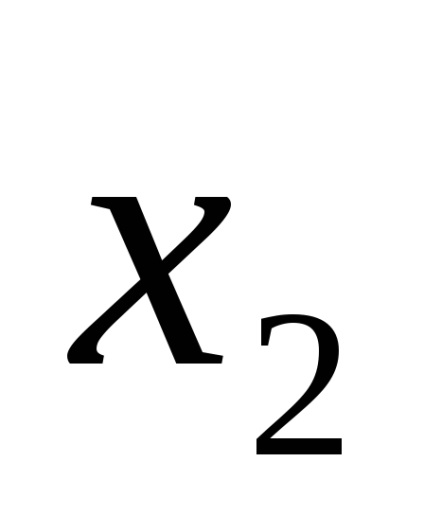
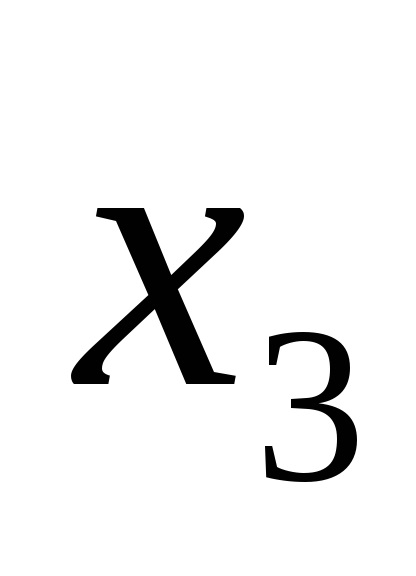
Folosirea formularelor normale nu elimină complet ambiguitatea scrierii funcțiilor logice. De exemplu, funcția (4) poate fi scrisă și ca:
Prin urmare, printre formele normale sunt cele în care funcțiile sunt scrise într-un mod unic. Ele sunt numite perfecte. Se utilizează forme normale disjunctive și perfect conjugate (SDNF și SKNF). Formele CDNF și SKNF au două caracteristici distinctive:
toate conjuncțiile elementare și disjuncțiile au același rang;
în conjuncții elementare (disjuncții), toate aceste variabile sau negațiile lor, de care depinde funcția, intră.
Funcția (5) conține conjuncții de același rang, dar este scrisă în DNF, nu în CDNF. Acest lucru se datorează faptului că conjuncțiile elementare nu conțin toate acele variabile sau negațiile lor, de care depinde funcția.
Funcția F (
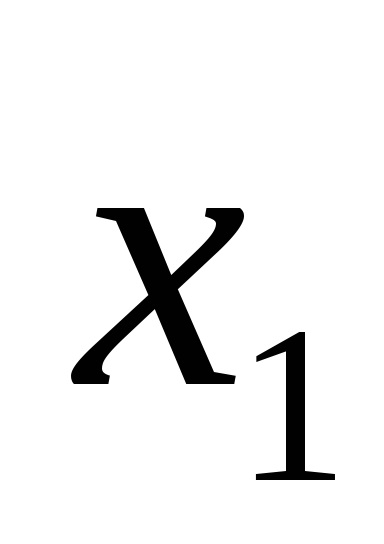
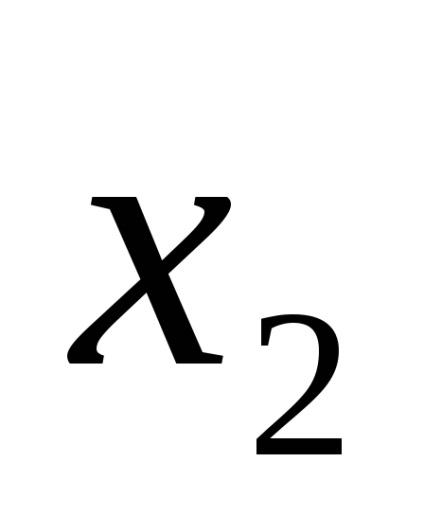
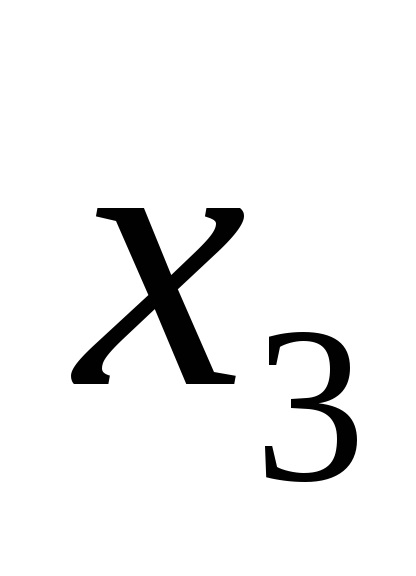
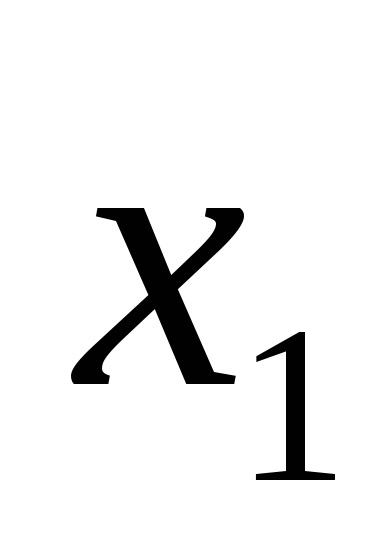
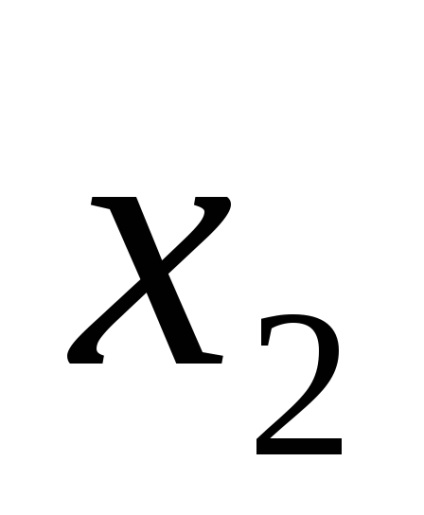
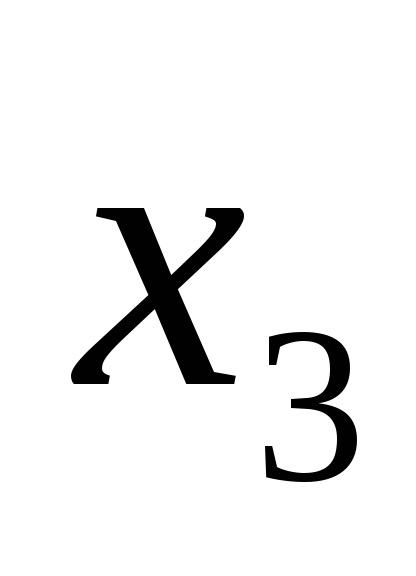
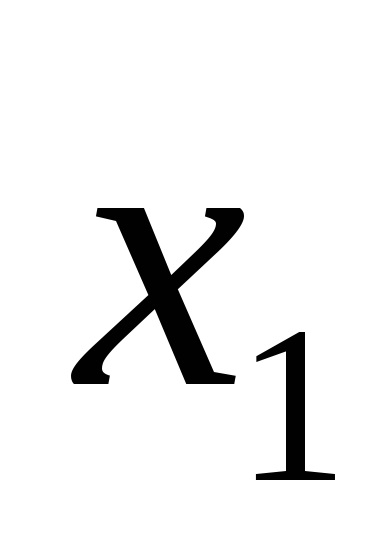
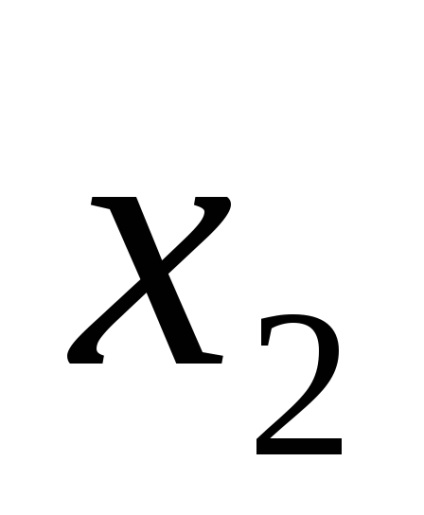
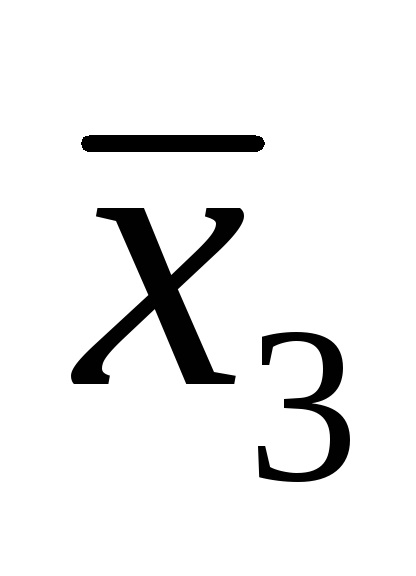
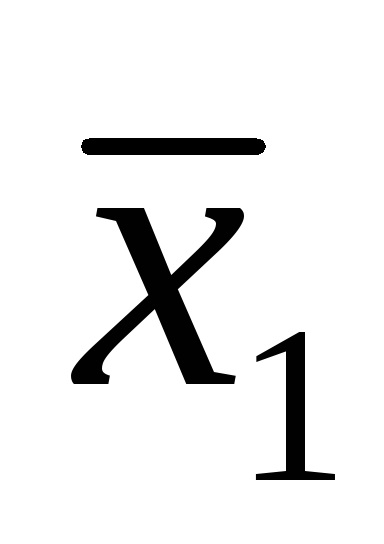
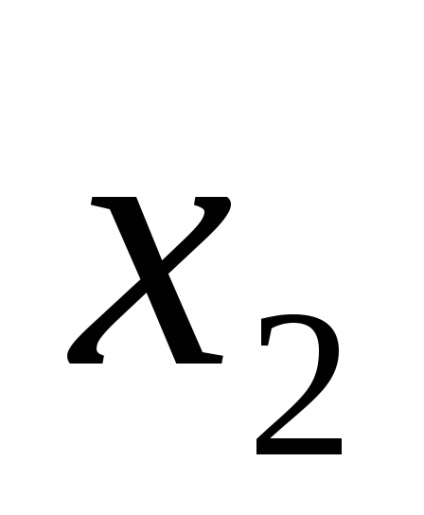
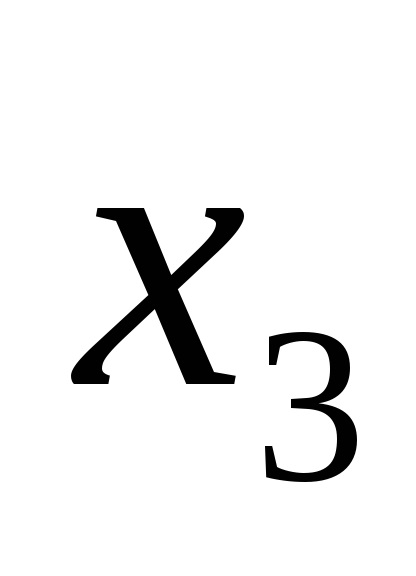
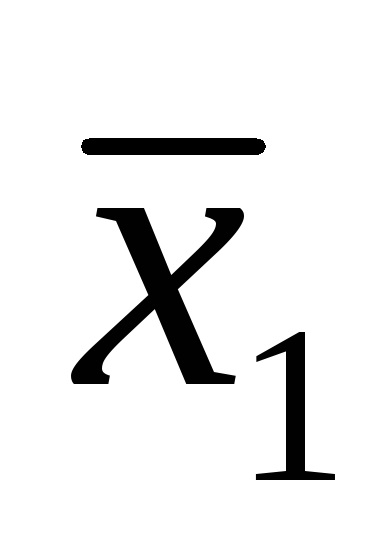
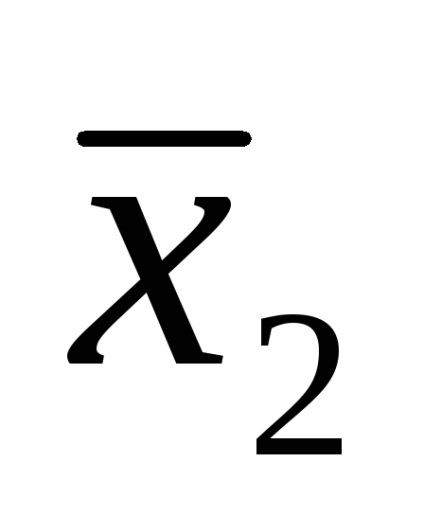
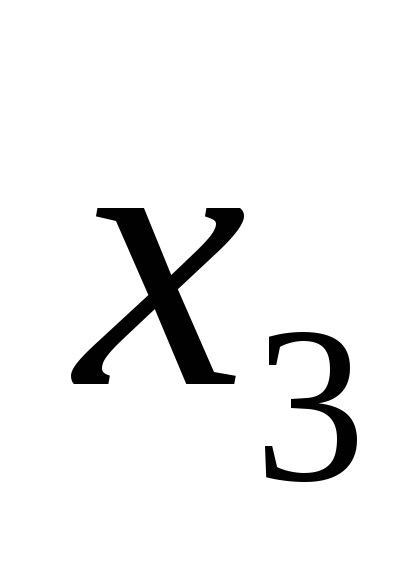
Funcțiile în CDNF și SKNF sunt de obicei scrise conform tabelelor cu adevăruri în conformitate cu anumite reguli.
1. Regula de înregistrare a funcției CDNF în conformitate cu tabelul de adevăr:
Pentru toate seturile de variabile pe care funcția ia valori unitare, scrieți conjuncțiile inversând acele variabile la care corespund valorile zero. Apoi conectați conjuncțiile cu semnele de disjuncție.
De exemplu, funcția logică este dată de tabelul de adevăr prezentat în Fig. 9a. Pentru seturile 3, 5, 6, 7, scriem conjuncții printr-un spațiu:
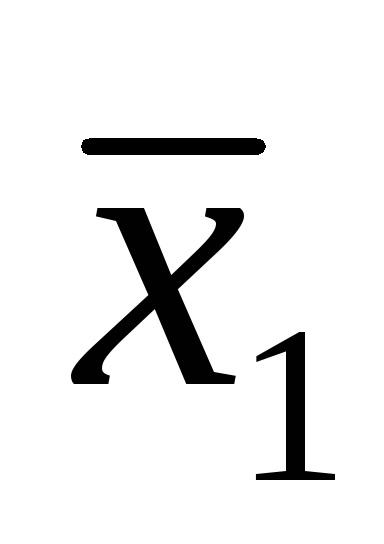
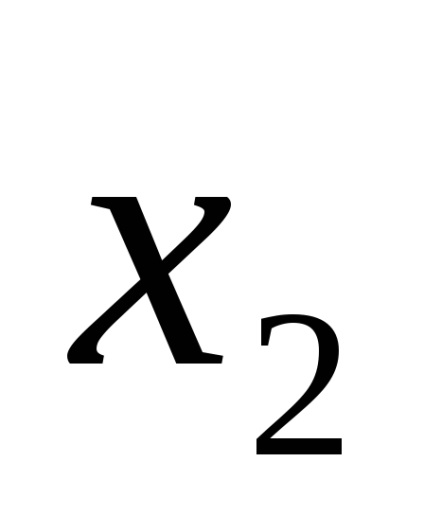
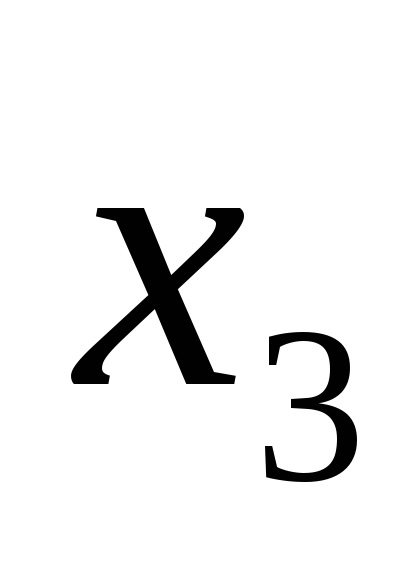
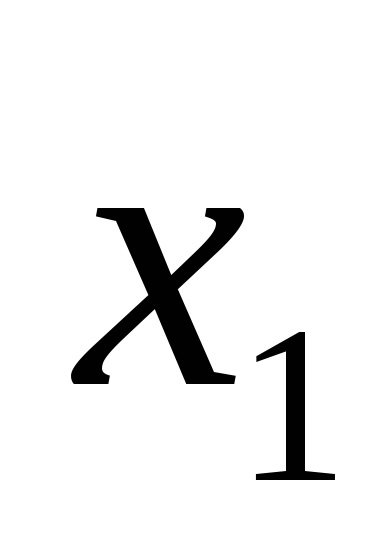
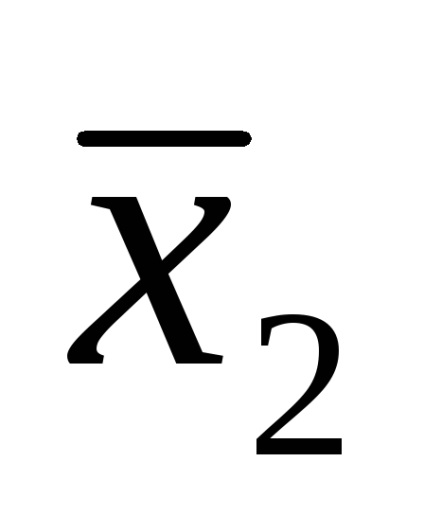
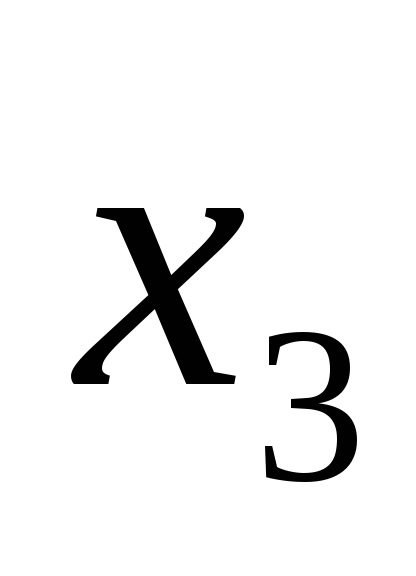
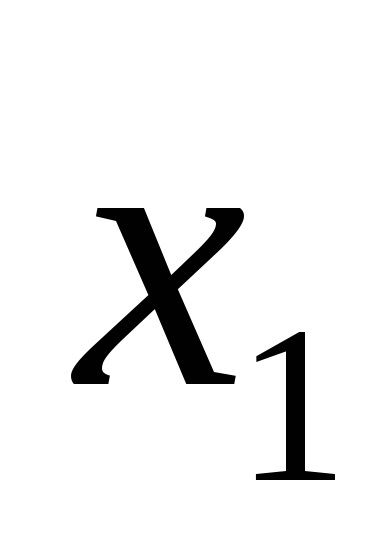
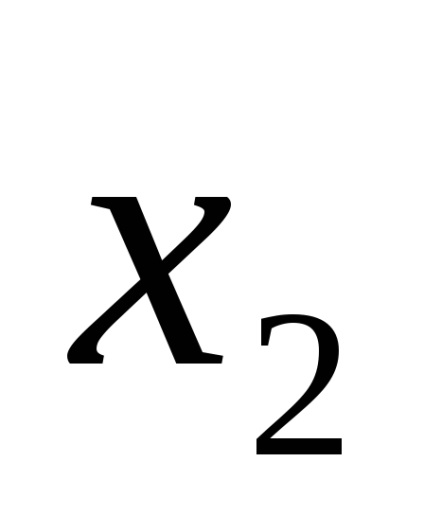
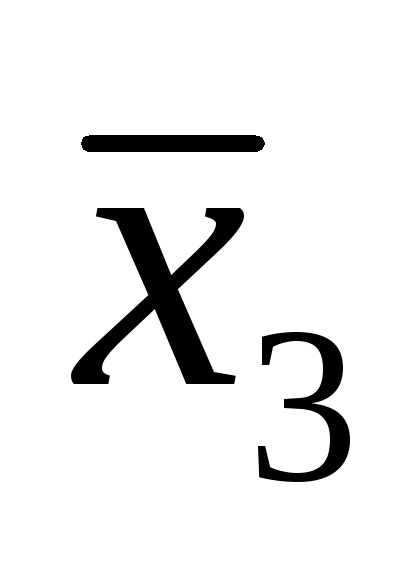
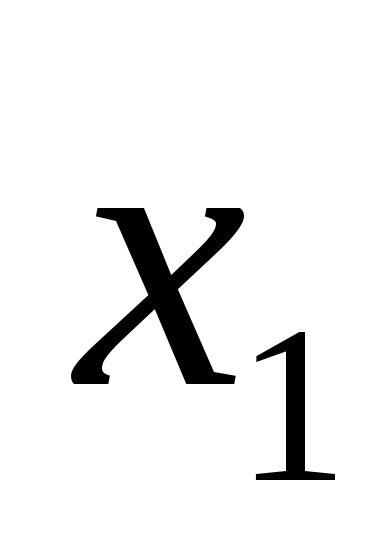
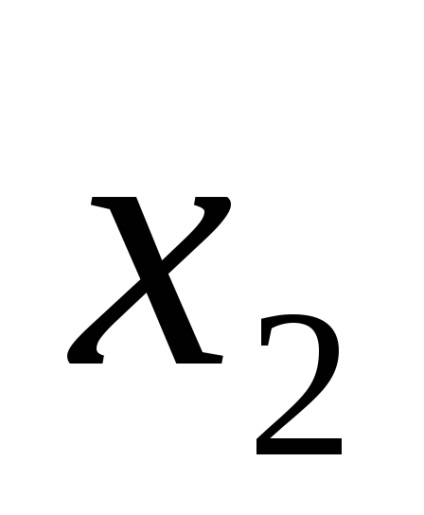
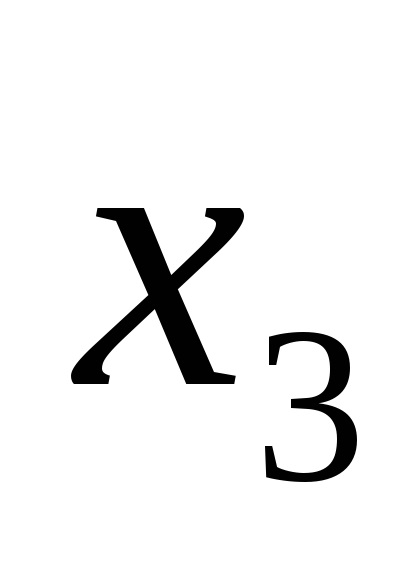
Plasăm semnul de disjuncție în blancuri și obținem o funcție în SDNF, adică F (