Pentru a simplifica expresia arcsin (x) + arcsin (-x) sau arctg (x) + arctg (-x), este suficient să ne amintim doar o proprietate a arcsinus (arctangent).
arcsin (-x) = - arcsin (x), arctg (-x) = - arctg (x). prin urmare
arcsin (x) + arcsin (-x) = arcsin (x) -arcsin (x) = 0,
arctg (-x) + arctg (x) = 0.
tg (arcsin (x) + arcsin (-x)) = tan 0 = 0,
sin (arcsin (x) + arcsin (-x)) = sin 0 = 0,
cos (arcsin (x) + arcsin (-x)) = cos 0 = 1,
tg (arctg (-x) + arctg (x)) = tan 0 = 0,
sin (arctg (-x) + arctg (x)) = sin 0 = 0,
cos (arctg (-x) + arctg (x)) = cos 0 = 1.
Dacă trebuie să construim un grafic al funcției y = arcsin (-x) + arcsin (x), începem soluția prin găsirea domeniului de definiție.
Domeniul de definire a unei funcții date coincide cu domeniul definiției funcției y = arcsin (x):
Astfel, graficul funcției y = arcsin (-x) + arcsin (x) se reduce la graficul funcției y liniară = 0 și reprezintă un segment de linie situată pe axa Ox cu puncte finale x = 1 și x = 1:
Graficele Funcția y = sin (arcsin (-x) + arcsin (x)) și y = tg (arcsin (-x) + arcsin (x)) reprezintă, de asemenea, segmente de la x = -1 până la x = 1, situată pe axa bou. Deși în găsirea domeniului celei de-a doua funcții, luăm în considerare faptul că tangenta nu este definită în punctele formei
nici unul dintre aceste puncte nu aparține unui segment de la -1 la 1.
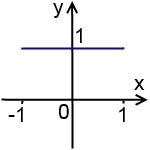
Graficul grafului funcției y = cos (arcsin (-x) + arcsin (x)) este segmentul liniei y = 1 cu capete la x = -1 și x = 1:
arccos (-x) = P-arccos (x), arcctg (-x) = P-arcctg (x). prin urmare
arccos (x) + arccos (x) = arccos (x) + arccos (x) = π,
arcctg (-x) + arcctg (x) = π-arcctg (x) + arcctg (x) = Π.
sin (arccos (-x) + arccoși (x)) = păcat π = 0,
cos (arccos (-x) + arccoși (x)) = cos Π = -1,
tg (arccos (-x) + arccoși (x)) = tg Π = 0,
sin (arcctg (-x) + arcctg (x)) = sin = π = 0,
cos (arcctg (-x) + arcctg (x)) = cos P = -1,
tg (arcctg (-x) + arcctg (x)) = tg P = 0.
Domeniul funcției y = arccos (-x) + arccos (x) -
Graficul grafic al funcției este un segment de la x = -1 la x = 1 - o parte din linia y = P:
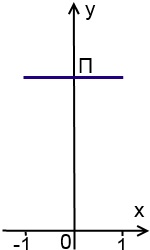
y = arccos (-x) + arcuși (x)
Graficul grafului funcției y = arcctg (-x) + arcctg (x) este linia y = P (domeniul arccotangent este linia întregului număr):
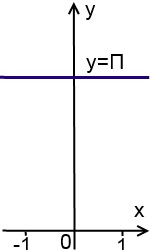
Graful = tg y (arctg (x) + arctg (-x)) - linie dreaptă y = 0 (adică, boului axa) înțepat x = P / 2 + Pn, unde n - întregi:
y = tg (arctg (x) + arctg (-x))
y = tg (arcctg (x) + arcctg (-x))
Graficul grafic al funcției y = tg (arcctg (x) + arcctg (-x)) este aceeași linie dreaptă.
Graficele Funcția y = sin (arctg (x) + arctg (-x)) și y = sin (arcctg (x) + arcctg (-x)) reprezintă un y = 0 (adică, bou axa) directă.
Graficul grafului funcției y = ctg (arcctg (x) + arcctg (-x)) este linia dreaptă y = 0 cu punctele punctate