Conform legii proporționalității de masă și energie, energia fotonului este egală cu
unde c este viteza luminii în vid.
Conform ipotezei Planck, energia fotonică este
Din aceste ecuații obținem expresii pentru masa fotonică
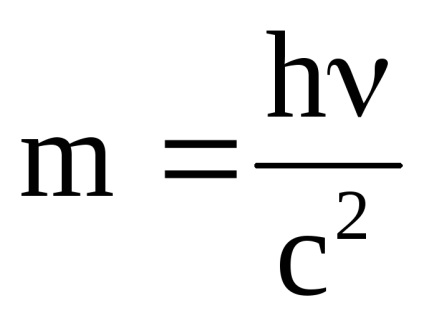
luând în considerare acest lucru
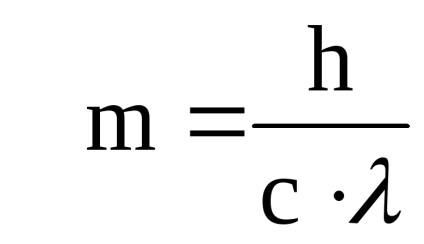
Expresia pentru impulsul p în forma generală:
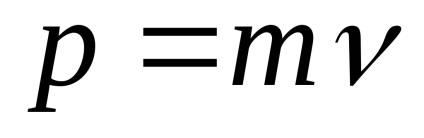
Masa restului fotonului este zero. Cuantumul radiației electromagnetice există doar propagând în spațiu la viteza luminii.
Deoarece un foton are un impuls, lumina care cade pe suprafata corpurilor trebuie sa exercite presiune. Fie un flux de fotoni, al cărui număr este egal cu Nφ, să cadă pe suprafața s = 1 m 2 a corpului opac într-un timp Δt = 1с. Dacă suprafața corpului are un coeficient de reflexie ρ, atunci fotnii ρNφ reflectă din el și (1 - ρ) Nφ este absorbit de corp. Fiecare foton reflectat va transmite impulsului p1 corpului. egală cu modificarea momentului acestui foton, adică
p1 =
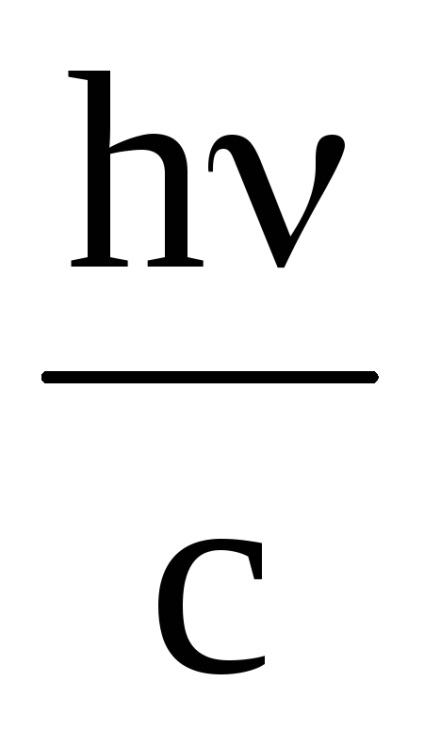
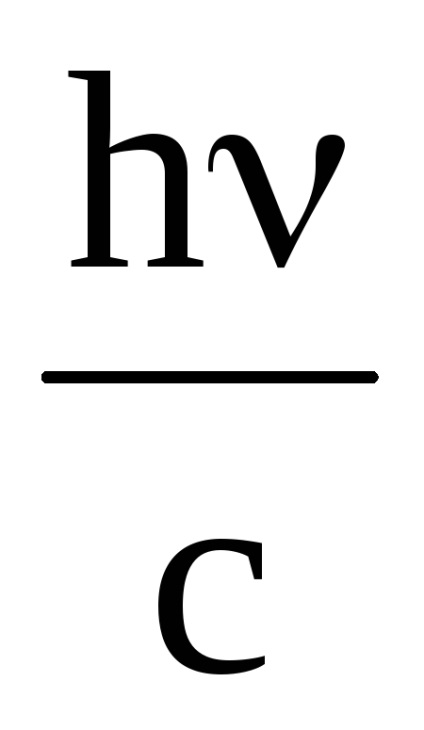
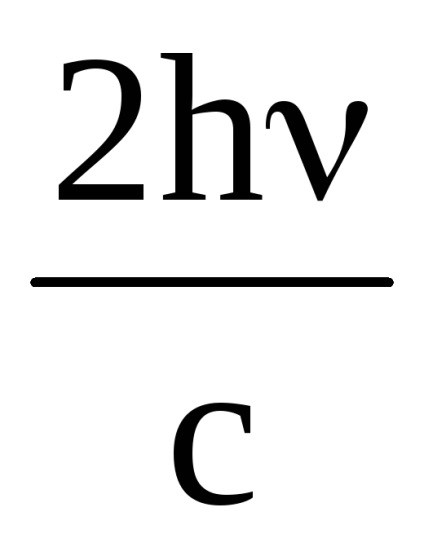
Momentul total obținut cu 1 m 2 de suprafață în 1 s este egal cu p
p = p1 · ρNφ + p2 (1 - ρ) Nφ =
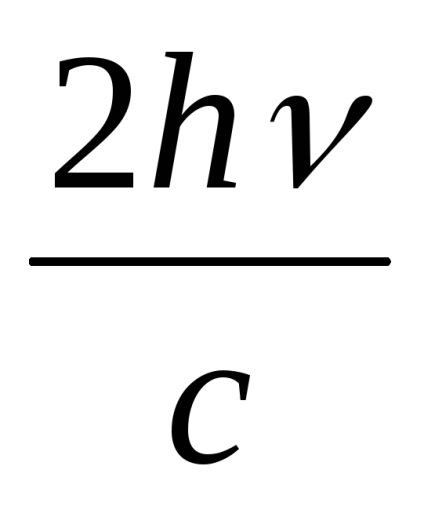
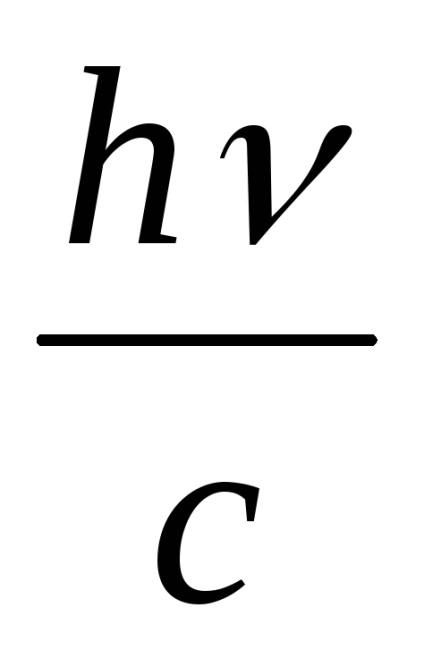
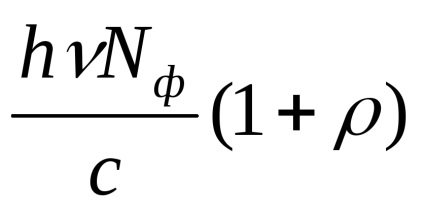
Presiunea va fi egală cu impulsul forței impuse de fotoni la o unitate de suprafață în 1 s. De aici rezultă că impulsul total primit cu 1 m 2 pe secundă este numeric egal cu presiunea P.
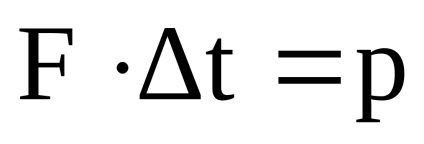
valoare


Această expresie pentru presiunea luminii este obținută din teoria cuantică a luminii.
O expresie a presiunii luminii poate fi obținută folosind noua teorie a luminii. Dacă suprafața metalică este în mod normal incidente undelor electromagnetice, intensitatea câmpului electric (E) de electroni se vor deplasa în direcția opusă direcției vectorului E. În acest caz, de câmpul magnetic al undei de lumină cu lumina de inducție a valului B pe fiecare electron-dy se deplasează cu forța v va fi acționată de forța Lorentz FI = evB, direcționată în interiorul metalului perpendicular pe suprafața sa. Astfel, un val de lumină va produce presiune pe suprafața metalică. Conform calculelor efectuate asupra teoriei electromagnetice a lui Maxwell, presiunea ușoară este exprimată prin formula
unde EE este iluminarea energetică a suprafeței, adică densitatea de flux a energiei luminoase care intră pe o anumită suprafață. Astfel, presiunea luminii este explicată cu succes atât de teoria undelor, cât și de teoria cuantică.
Efectul Compton
Împrăștierea radiației electromagnetice în electroni liberi sau slab fixate, în care un singur foton în coliziune elastic rezultate-Tate Transferurile de electroni parte nume său sa inimă și energie, numit efectul Compton (Pentru primele-tiile observate în 1923.) efectul Compton arată că fotonii , în ciuda naturii undelor, se comportă ca particule și sunt capabile să interacționeze cu alte particule în conformitate cu principiul asemănător cu impactul bilelor elastice.
Un foton incident cu hν energie (Fig. 163), ca rezultat al coliziunile treceri lor de electroni de energie si este transformata in alt hν energia fotonică“, care se mișcă într-un unghi de Θ față de direcția inițială de mișcare a fotonului.
Conform legii de conservare a energiei cantitatea de hv energie primară a energiei fotonice a unui electron în repaus și E0 = M0 c 2 trebuie să fie egală cu suma dintre energia hν foton împrăștiată „și energia deplină a electronului după ciocnire
hν + m0 c 2 = hν '+ mc 2. unde
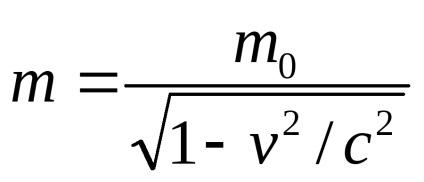
În procesul de coliziune a unui electron și a unui foton, legea conservării impulsului
p și pE sunt momenta inițială a unui foton și a unui electron, p 'și p' e momenta lor după împrăștiere.
Presupunem că viteza inițială a electronului era zero. Apoi pE = 0. Momentul fotonului p =
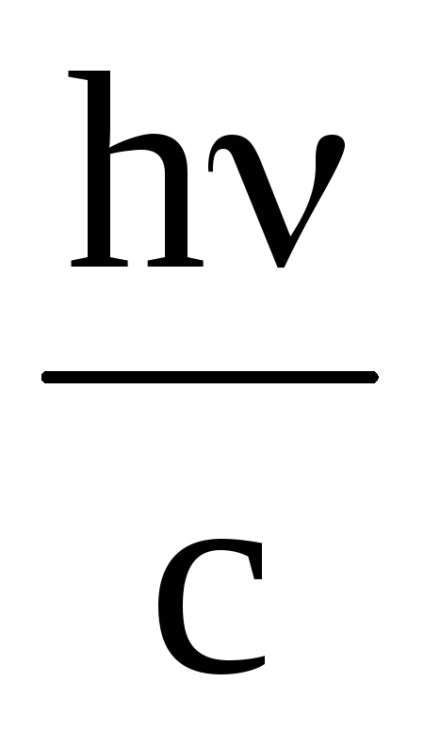
unde h este constanta lui Planck; ν și ν 'sunt frecvențele incidentului și împrăștiate
și
Din diagrama vectorială a impulsurilor (Figura 164) rezultă că:
Rezolvarea în comun a ecuațiilor 1 și 2, ținând seama de faptul că
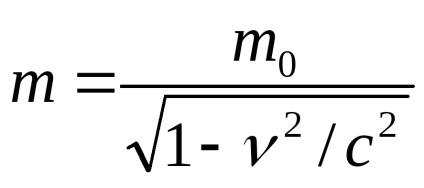
.
Luând în considerare acest lucru și tăind cu c, ajungem
.
valoare
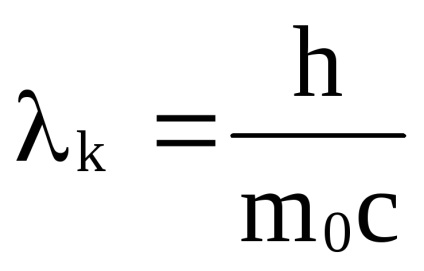
Energia cinetică a electronului de recul (după interacțiunea cu fotonul) va fi
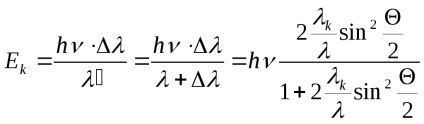
Electronul de recul atinge energia maximă la Θ = π, adică când fotonul este împrăștiat în direcția opusă
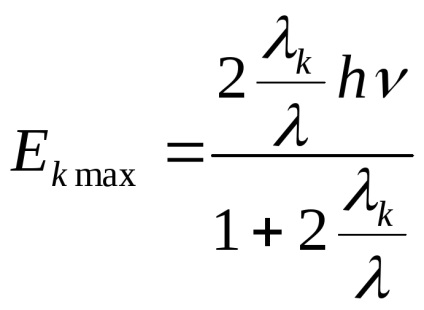
Absorbția unui foton de către un electron liber este imposibilă, deoarece Un astfel de proces contravine legilor conservării energiei și impulsului.
Aceste două relații sunt compatibile numai pentru ν = 0.