Utilizăm ecuația (4) și luăm din ea derivatul timpului
În (8) pentru vectorii unitari există proiecții ale vectorului de viteză pe axele de coordonate
Proiecțiile de viteză pe axele de coordonate sunt definite ca fiind prima dată derivate ale coordonatelor corespunzătoare.
Cunoscând proiecția, puteți găsi modulul vectorului și direcția sa
Determinarea vitezei cu metoda naturala
Să fie dată traiectoria punctului material și legea schimbării coordonatei curbilinii. Să presupunem că, pentru t1, punctul a avut
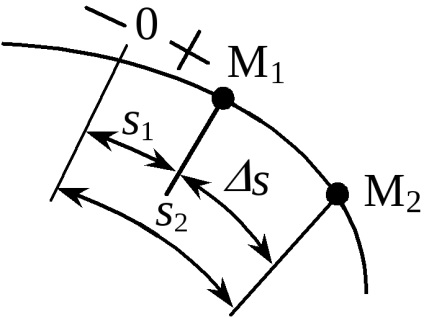
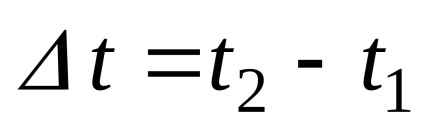
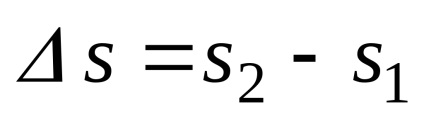
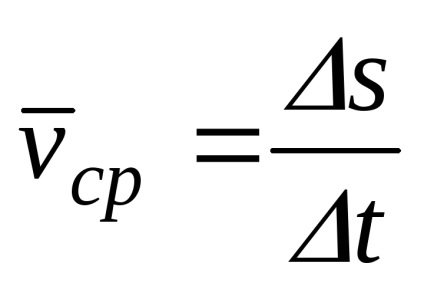
Pentru a găsi viteza într-o anumită clipă de timp, trecem la limită
,
Vectorul de viteză al unui punct sub metoda naturală de specificare a mișcării este definit ca prima derivă a unei coordonate curbilinii.
Prin accelerarea unui punct material se înțelege o cantitate vectorică care caracterizează rapiditatea schimbării vectorului de viteză a unui punct în magnitudine și direcție cu trecerea timpului.
Accelerarea punctului cu modul vectorial de mișcare
Luați în considerare un punct la două puncte în timp t1 (
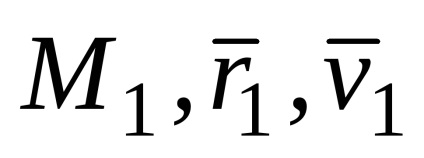
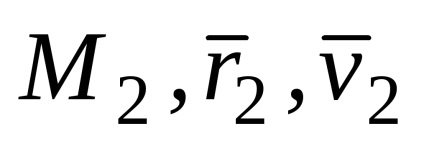
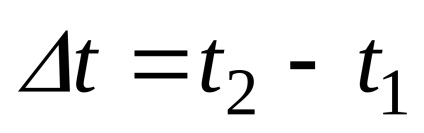
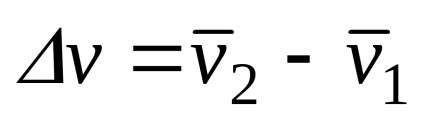
vector

P
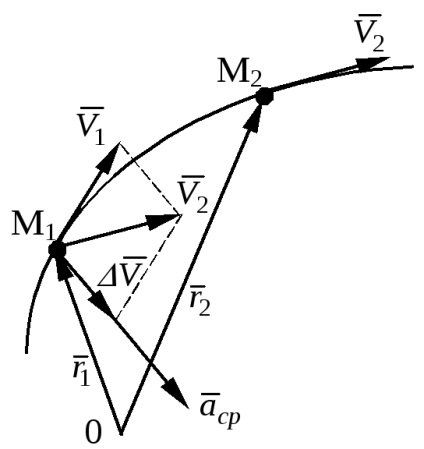
Pentru a găsi accelerația într-o anumită clipă de timp, trecem la limită
,
Accelerația unui punct la un moment dat este definită ca a doua derivare a vectorului de rază a punctului sau a primului derivat al vectorului de viteză în raport cu timpul.
Vectorul de accelerație este situat în planul contiguu și îndreaptă spre concavitatea traiectoriei.
Accelerarea unui punct în metoda coordonatelor de specificare a mișcării
Folosim ecuația cuplării vectorului și coordonează metodele de specificare a mișcării
.
Și luăm din el al doilea derivat
,
În ecuația (15), pentru vectorii unitari, proiecțiile vectorului de accelerație pe axele de coordonate
Proiecțiile de accelerație pe axele de coordonate sunt definite ca fiind prima dată derivate ale proiecțiilor de viteză sau ca derivate secundare ale coordonatelor de timp corespunzătoare.
Modulul și direcția vectorului de accelerare pot fi găsite din următoarele expresii
Accelerarea punctului în modul natural de stabilire a mișcării
P
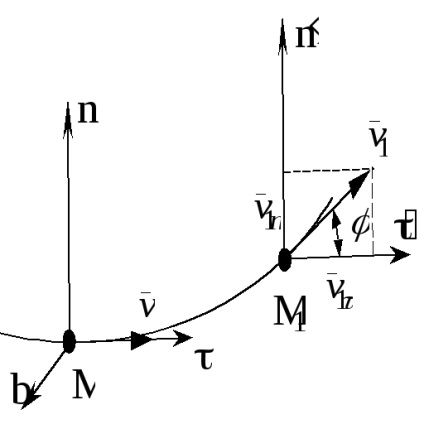
Accelerația în acest caz este determinată prin proiecția sa pe axa sistemului natural de coordonate care se deplasează cu punctul M. Axele sunt astfel direcționate după cum urmează:
M este tangenta, este dirijata de-a lungul tangentei catre traiectorie, spre numarul pozitiv al distantei,
Mn - principala normală, este îndreptată de-a lungul normalei situată în planul contiguat și este îndreptată spre concavitatea traiectoriei,
Mb - binormal, perpendicular pe planul Mătn și formează dreapta trei cu primele axe.
Deoarece vectorul de accelerație se află în planul contiguat, atunci ab = 0. Gasim proiecțiile accelerației pe alte axe.
Proiectam (19) axele de coordonate
Trageți prin punctul M1 axele paralele cu axele din punctul M și găsiți proiecțiile de viteză:
unde este așa-numitul unghi de adiacent.
Înlocuim (22) în (20)

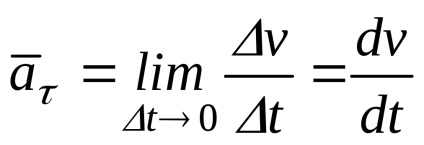
Accelerarea tangențială a unui punct este determinată de derivatul de viteză pentru prima dată a vitezei sau de al doilea derivat de timp al coordonatei curbilinii.
Accelerarea tangențială caracterizează schimbarea vectorului de viteză în magnitudine.
Înlocuim (22) în (21)
.
Înmulțiți numitorul și numitorul cu s pentru a obține limite cunoscute
unde
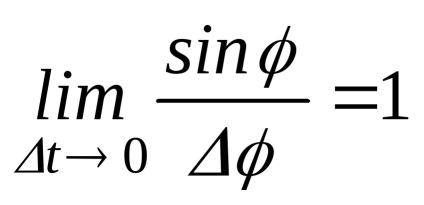
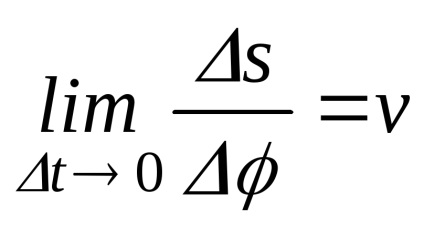
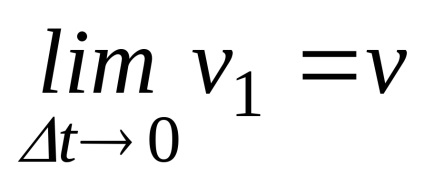
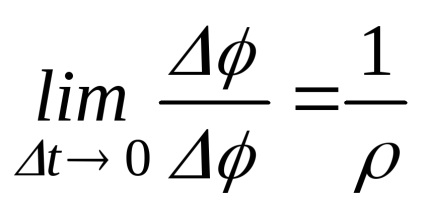
Înlocuindu-ne limitele calculate în (24), obținem
Accelerația normală a unui punct este determinată de raportul dintre pătratul vitezei și raza de curbură a traiectoriei la un anumit punct.
Accelerația normală caracterizează schimbarea vectorului de viteză de-a lungul direcției și este întotdeauna îndreptată spre concavitatea traiectoriei.
În cele din urmă, obținem proiecțiile de accelerare a punctului material pe axa sistemului natural de coordonate și modulul vectorului