Să găsim rezultatul a două forțe paralele care acționează asupra unui solid în două cazuri:
1. Forțele sunt direcționate într-o singură direcție.
Forța egală a două forțe paralele care acționează pe un corp absolut rigid, direcționată într-o direcție, este egală cu suma modulelor termenilor de forțe modulo, este paralelă și direcționată în aceeași direcție. Linia de acțiune a rezultatului trece între punctele de aplicare a termenilor forțelor la distanțe față de aceste puncte invers proporționale cu aceste forțe.
2. Forțele sunt direcționate în direcții diferite.
P
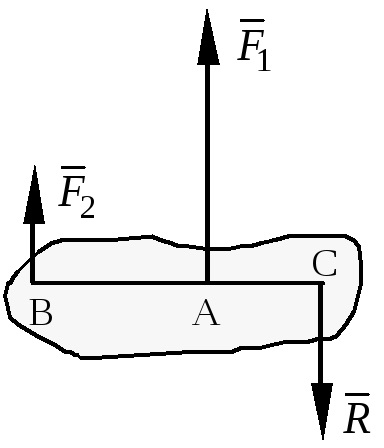
Cu ajutorul acestor formule este posibilă rezolvarea problemei extinderii forței în două paralele.
O pereche de forțe este un sistem de două forțe egale, modulo, paralele și opuse.
Planul care trece prin liniile de acțiune ale forțelor perechii se numește planul de acțiune al perechii.
Distanța dintre liniile de acțiune ale forțelor perechii se numește umărul perechii.
P
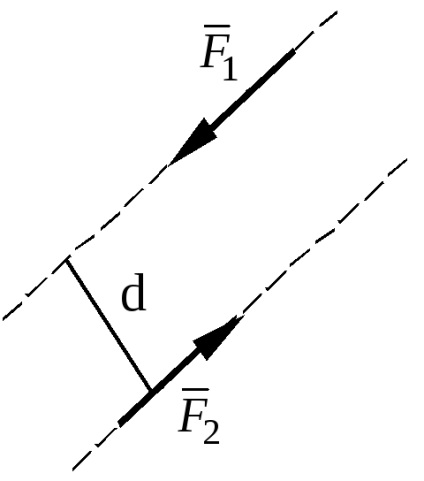
Momentul unei perechi de forțe este o cantitate egală cu produsul modulului unei forțe a perechii pe umăr, luată cu semnul corespunzător
Proprietățile unei perechi de forțe
1. Efectul unei perechi de forțe asupra corpului nu se va schimba dacă schimbă arbitrar forțele și umărul în același timp cu perechea.
2. Fără modificarea efectului unei perechi de forțe, ea poate fi transferată arbitrar în planul acțiunii sale.
3. O pereche de forțe poate fi rotită în planul acțiunii sale sub orice unghi.
4. Acțiunea mai multor perechi de forțe aplicate într-un plan poate fi înlocuită de o pereche de forțe, momentul fiind egal cu suma algebrică a momentelor perechilor de forțe date.
Condiția de echilibru pentru un sistem plan de forțe
Pentru echilibrul unui sistem de forță plană arbitrară, este necesar și suficient ca suma algebrică a proiecțiilor tuturor forțelor pe axele de coordonate și suma algebrică a momentelor tuturor forțelor față de orice punct să fie egală cu zero
Teorema transferului forței paralele
Teorema: Forța aplicată unui corp solid poate fi transferată paralel în orice punct al corpului, fără a schimba acțiunea care trebuie efectuată, adăugând o pereche cu un cuplu egal cu momentul forței transferate în raport cu punctul unde forța este transferată.
Reducerea unui sistem de forță plană într-un centru dat
Folosind teorema pentru transportul paralel, sistemul de forțe care acționează pe un corp solid poate fi transferat într-un singur punct. Acest punct va fi numit centrul de reducere.
În acest caz, forța
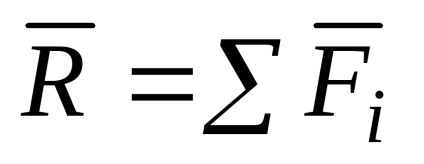
Teorema: Fiecare sistem de plată a forțelor, atunci când este activat la un sistem de vector egal principal arbitrar audio tsentruOzamenyaetsya siloyR și aplicate pentru a aduce centru, și cu o pereche momentomMO egală cu punctul principal al sistemului relativ tsentraO.