1 Piramida corectă a fost pregătită de profesorul de matematică Korepanov ZI.

2 Pe piramida Termenul piramidă este împrumutat de la piramidele sau piramidele grecești. Grecii, la rândul lor, au împrumutat acest cuvânt, se crede, din limba egipteană. În papirusul lui Ahmes, cuvântul piramă se găsește în sensul marginii piramidei obișnuite. Alții cred că termenul provine din formele de pâine din Grecia antică, pirozis). Datorită faptului că forma flacării seamănă uneori cu imaginea unei piramide, unii oameni de știință medievali credeau că termenul provine de la cuvântul grecesc - sărbătoarea. De aceea, în unele manuale de geometrie ale secolului al XVI-lea. Piramida este numită corpul focului.

3 Euclidul piramidal definește ca o figură solidă mărginită de planuri care converg de la un plan (bază) la un punct (vârf). Această definiție a fost criticată deja în antichitate, de exemplu, de Geron, care a propus următoarea definiție a piramidei. este o figură mărginită de triunghiuri care converg la un punct și a cărei bază este poligonul. Piramidă patrulaterală

4 Un poliedron, una dintre fețele căreia este un poligon, iar celelalte fețe sunt triunghiuri cu un vârf comun, se numește o piramidă. O piramidă a cărei bază este un poligon regulat și un vârf proiectat în centrul său este numit corect.

5 este un polyhedron constând dintr-un n-gon A 1 A 2 A 3. Un n (bază) și n triunghiuri (fețe laterale) având un vârf comun (P). P A1A1 A2A2 A3A3 AnAnH PA1; PA 2; PA 3; ; PA n - marginile laterale A 1 A 2 ;. ; А 1 А n - marginile bazei РН - înălțimea piramidei - h h

6 baza este un poligon obișnuit, vârful este proiectat în centrul bazei; marginile laterale sunt egale; fețe laterale - triunghiuri egale cu egalitate egală. H - înălțime, h - apophema H h
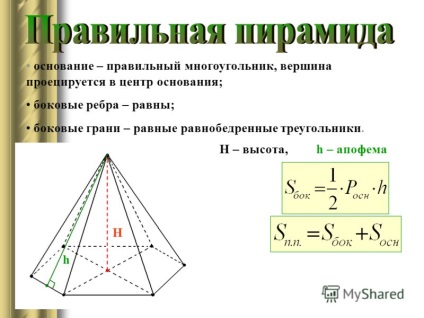
7 AB = BC = AC = a Piramida triunghiulară corectă H - înălțimea, h - apophema A O B C h H S D a
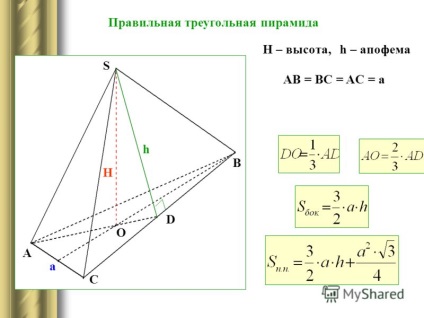
8 Piramida quadrangulară corectă h - apophema, H - înălțimea, AB = BC = CD = DA = a (baza - pătrat) H h a a A B D O P K K - mijlocul DC C a -
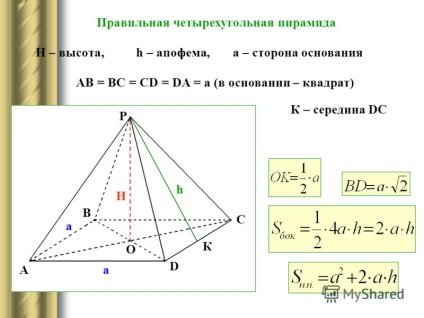
9 Având în vedere: MAVCD este piramida corectă. Construiți: (AM; ABCD). Construcție: MO ABCD; AO este proiecția AD în planul de bază; (AM; ABCD) = MAO.
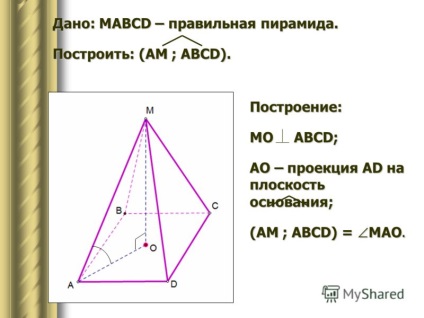
10 Având în vedere: MAVCD este piramida corectă. Construiți: (CMD; ABCD). Construcție: Vom conduce apogeul MN. MO AABD; DAR - proiecția MN pe ABCD. Prin urmare, CD-ul nu este. (SMB; ABCD) = MNO.
11 Având în vedere: MAVCD este piramida corectă. Pentru a construi: (АВМ; BMC). Construcție: 1) OK MB; 2) MB AC, MB AC; 3) MB AKC; 4) AK MB; CK MB; 5) (ABM; BMC) = AKC.
12 Exemple de piramide În natură În arhitectură În construcții
13 piramide egiptene (în mijlocul piramidei lui Cheops a cărei înălțime atinge 147 m)
14 La periferia Cairo - capitala Egiptului modern, este cel mai înalt - Piramida lui Keops
15 America Centrală la nord de orașul Mexico City Teotiukan Piramida soarelui
16 Insula Tenerife: Piramidele din Guimar
17 Pe fundalul lanțului muntos Himalaya iese în evidență în mod clar educație piramidal - Mount Kailash
19 Frankfurt: o casă de țară în 1896. Una dintre turnuri are forma unei piramide și conferă clădirii un aspect maiestuos.