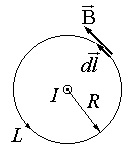
După cum vedem, circulația B nu depinde de raza cercului, ci este determinată numai de curentul pe care îl mărește. Se poate demonstra că această proprietate a câmpului magnetic rămâne validă și pentru cazul unui contur de integrare arbitrară L. și, de asemenea, în cazul în care mai multe curenți curg prin zona S (vezi Fig.
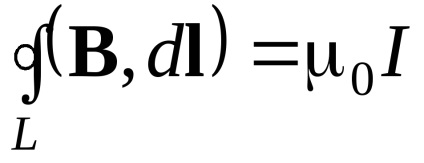

Aplicăm legea curentului total pentru un cerc infinitezimal al zonei dS. prin care curge un curent infinitezimal dI. Folosind formula care exprimă curentul printr-un tampon prin densitatea curentului, adică dI = jdS, obținem legea curentului total în forma diferențială:
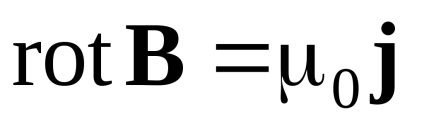

Să comparăm ecuațiile diferențiale pentru un câmp magnetic cu ecuațiile diferențiale care descriu un câmp electrostatic (în vid):
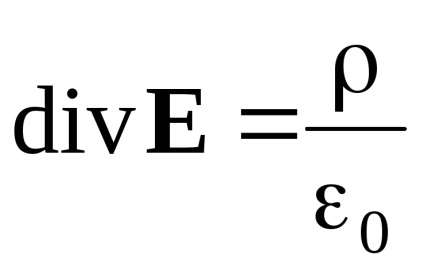
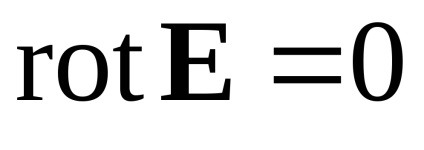
Diferența câmpului electrostatic nu este zero în regiunea sursă. Liniile de forță ale câmpului electric încep cu încărcături pozitive și se termină cu sarcini negative. Diferența câmpului magnetic este zero peste tot. Liniile magnetice de forță din afara surselor câmpului magnetic sunt închise (în câmpul surselor de câmp nu au sens deloc). Rotorul câmpului electrostatic, ca și circulația acestuia, este identic zero. În orice moment, vectorul forței câmpului electrostatic este exprimat în funcție de gradientul unei anumite funcții scalare, numit potențial. Câmpul electrostatic este potențial. Rotorul B nu este egal cu zero în regiunea sursă. Din acest motiv, circulația B nu este, de asemenea, zero în această regiune. Vectorul B nu este un gradient al oricărei funcții de coordonate scalare. Câmpul magnetic, prin urmare, este nonpotențial (este vortex) ..
Deci, curenții electrici (mișcarea de încărcare direcționată) creează un câmp magnetic și
sarcini necompensate - câmp electrostatic. În interiorul conductorului există un câmp electric datorită prezenței EMF în circuit cu curentul. Un conductor este înconjurat de un câmp magnetic, care se găsește prin legea Biot-Savart-Laplace