e (t), e1 (t) sunt cantitățile de intrare
i3 este valoarea de ieșire
1. Construirea unui model matematic de management
1. 1 Construirea unui model matematic pentru circuitul electric
Să stăm modelul matematic al obiectului de control în spațiul de stare. Diagrama structurala a obiectului de control:
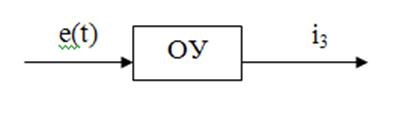
În schemă, patru elemente, stocarea energiei, prin urmare modelul matematic ar trebui să fie de ordinul al patrulea.
1.2 Construirea unui model matematic:
Facem patru ecuații de-a doua lege a Kirchhoff la contururile și de a găsi un sistem de ecuații care descriu obiectul metodei de control al curenților de buclă:
În sistemul inițial de ecuații, trebuie să scăpăm de toate integralele, diferențiind ecuațiile.
Se scapă de integrale în ultima ecuație a sistemului (2):
Folosind metoda integrării condiționale, este necesar să se introducă variabile fictive egale cu elementele luate din ecuație, dar cu 1 sau mai multe ordine de mărime mai mici.
În cazul nostru, folosind metoda de integrare condiționată, introducând variabile dummy elemente egale preluate din ecuația (3), pe ordinea de 1 și 2 de mai jos, și din 2 și setul de ecuații a 3 (2):
Derivații în raport cu timpul din variabilele fictive se găsesc și, aplicând ecuațiile anterioare, sunt exprimate de dependențele curenților variabilelor fictive.
Din sistemul (4) și din prima ecuație a sistemului (2), exprimăm curenții astfel încât să depindă numai de variabilele inactivi.
Expresiile curente rezultate sunt substituite în sistem (5) și completate cu o expresie pentru cantitatea de ieșire, ca rezultat obținem:
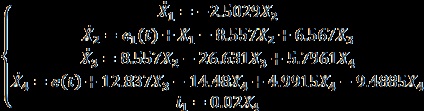
Pe baza sistemului de ecuații obținut și a ecuației pentru valoarea de ieșire a obiectului de control, este scris un model matematic în forma normală a lui Cauchy:
-ecuația valorii de ieșire a obiectului,
unde A, B, C, D sunt matrici;
X este matricea variabilelor interne;
U este matricea variabilelor de intrare, în acest caz U este EMF.
În acest caz, matricile vor arăta astfel:
Obținem un model matematic în spațiul de stare
1.3 Construcția graficului sistemului și determinarea funcției de transfer
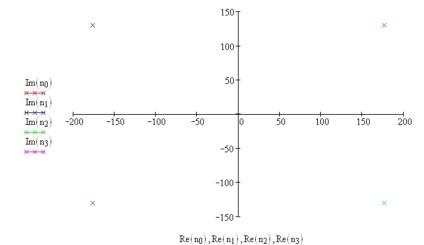
Fig. 9 Graficul rădăcinilor lui n în planul complex
Din rădăcinile jumătății superioare se formează expresia pentru:
Deoarece factorul numitor este format din soluția de ecuație
atunci ea poate fi înlocuită direct de această ecuație. Avem:
Transformăm de la iω la p:
După rezultate similare, vom primi funcția de transfer a filtrului de formare:
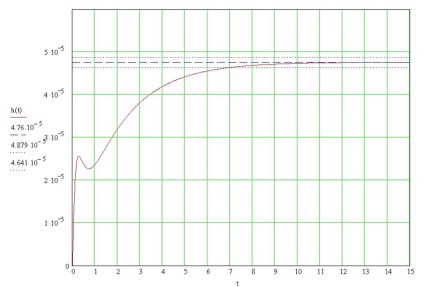
h (t) este valoarea staționară a procesului tranzitoriu
h (t) max = - valoarea maximă a procesului tranzitoriu
tpp = 7 s - Timp tranzitoriu
toc = 12 s - Timpul primului acord
tnar = 12 s - Timpul de creștere
n = 0 - Numărul de oscilații
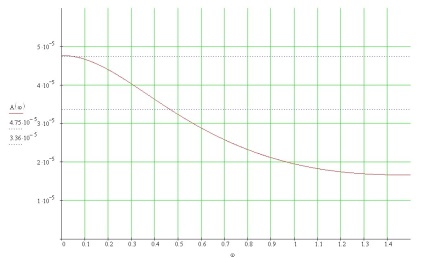
Fig. 11 Graficul de răspuns al frecvenței