Trei puncte în spațiu. și. Nu mint pe o linie, definesc un singur plan. Este evident că un punct se află în acest plan dacă și numai dacă vectorii
sunt coplanare. În conformitate cu criteriul coplanarității, acest lucru este echivalent cu faptul că produsul mixt al acestor vectori este egal cu zero:
Ultima egalitate este ecuația planului care trece prin aceste trei puncte. Dacă scriem acest determinant (de exemplu, pe elementele primului rând), atunci obținem ecuația generală a planului.
atunci criteriul apartenenței la un punct al planului în cauză poate fi descris prin ecuația:
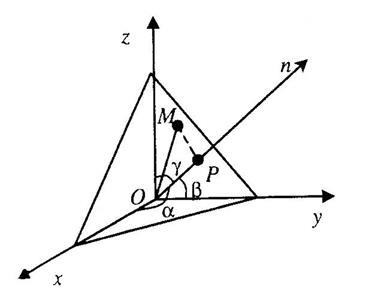
Ecuația rezultată este ecuația unui plan dat, numită ecuația sa normală.
Punctul de plecare al acestui plan este distanța de la acel punct la planul, luat cu semnul plus, în cazul în care punctul și minciuna de origine pe laturile opuse ale planului considerat, și a luat cu semnul minus, dacă punctul și minciuna de origine, pe de o parte a planului în cauză.
Luați în considerare un punct arbitrar de spațiu. Proiectăm acest punct pe un vector. Să fie proiecția rezultată. Abaterea unui punct dintr-un plan dat este. Este evident că
Cu alte cuvinte, pentru a găsi abaterea unui punct din plan, este necesar să se substituie în locul părții din stânga a ecuației normale a planului. și coordonatele acestui punct. Este evident că distanța de la un punct la un avion este definită de egalitate:
Observăm că ecuația generală a avionului
Acesta poate fi redus la o formă normală în același mod ca și în cazul ecuației unei linii drepte în plan. Pentru aceasta este necesar să alegeți un astfel de număr
Squaring primele trei egalități, adăugându-le și luând în considerare faptul că suma de pătrate a cosines direcție este una, vom obține:
Din egalitate rezultă că semnul trebuie ales opus semnului coeficientului liber. Numărul. definit în acest fel, se numește factor de normalizare. Dacă înmulțim ambele părți ale ecuației generale cu un factor de normalizare, obținem o ecuație normală. În concordanță cu aceste considerente, concluzionăm că distanța de la un punct la un avion este determinată de formula:
Un exemplu. Găsiți ecuația normală a planului care trece prin punctele. . .
# 8710; Utilizăm formula pentru găsirea ecuației unui plan care trece prin trei puncte date. și:
Ca rezultat, obținem:
Ecuația rezultată este o ecuație generală a planului. Noi o reducem la forma normală. În acest scop, găsim factorul de normalizare:
Înmulțim ambele părți ale ecuației generale a planului cu factorul de normalizare găsit:
Aceasta este ecuația normală a planului dat. ▲