Lucrări de laborator N 2.
DEFINIREA MOMENTULUI DE INERTIA A MAYANIK OBERBEK
Obiectiv: Pentru a determina momentul de inerție al pendulului Oberbeck, folosind legea conservării și transformării energiei și pentru a studia dependența momentului de inerție pe localizarea masei în păianjeni.
INSTRUMENTE ȘI ACCESORII
PREGĂTIREA PENTRU MUNCĂ
Pe prelegeri și pe lista literaturii pentru a studia următoarele întrebări teoretice:
TEORIA METODEI DE MĂSURĂRI ȘI DESCRIEREA INSTALĂRII
Pendulul Oberbeck (Figura 1) constă din patru tije și două scripeți de rază diferită, fixate pe o axă de rotație orizontală. Pe tije, o sarcină cu aceeași masă m 0 se poate mișca și se fixează în poziția dorită patru (câte una pe fiecare tija).
Una dintre rolele de rază r 1 sau R 2 înfășoară un fir, la capătul căruia este atașată o platformă cu încărcătură. Fie m 1 masa platformei și m 2 masa sarcinii, adică masa totală: m = m 1 + m 2.
În cazul în care marfa este m ridicat la o anumită înălțime h 1 și eliberat, sarcina se va deplasa, iar tensiunea a scripetelui fire de derulare TH creează un moment de rotație M. în dispunerea simetrică a mărfurilor pe traversei va fi singurul sistem de operare în cuplu.
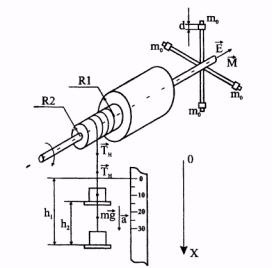
Să presupunem că la momentul inițial (t = 0) platforma fixă cu sarcina se află la o altitudine h 1. Energia mecanică totală a sarcinii va fi determinată de energia potențială:
Atunci când se deplasează încărcătura energie potențială este transformată în energie cinetică cu o platformă de marfă și energia cinetică de rotație a pendulului la momentul t 1. când platforma cu o sarcină adecvată în poziția inferioară, energia totală a sistemului, „Overbeck a pendulului și cu o platformă de încărcare“ este:
unde este energia cinetică a mișcării translaționale a platformei cu sarcina;
- energia cinetică a unui pendul rotativ;
I este momentul de inerție a pendulului față de axa de rotație.
Trebuie remarcat faptul că în poziția extremă (când firul este complet dezbracat), sarcina cu platforma continuă să se deplaseze în jos, provocând o deformare a firului elastic. În acest caz, energia cinetică a sarcinii trece în energia potențială a deformării filamentului. Când încărcătura se mișcă în sus, energia potențială devine din nou energia cinetică a încărcăturii.
În timpul rotirii pendulului și a mișcării încărcăturii, forța de rezistență la aer acționează, iar în lagăre, forța de frecare acționează asupra axei de rotație. Fie ca toate aceste forțe să determine momentul total al forței de frecare Mtr. Prezența unei forțe de frecare încalcă legea conservării energiei mecanice, deoarece o parte din ea trece în energie internă
Lucrarea forței de frecare la rotirea pendulului:
unde este unghiul de rotație al volantului atunci când platforma este deplasată cu sarcina pe o distanță h 1.
unde R este raza roții
Conform legii conservării energiei totale:
unde este schimbarea energiei totale în timpul tranziției platformei de la punctul superior la cel inferior:
Pendulul continuă să se rotească în aceeași direcție și ridică platforma cu sarcina la o înălțime de h 2. unde h 2 Pierderea energiei totale este egală cu forța forțelor de frecare în timpul rotației de-a lungul întregii căi de mișcare în jos și în sus: Sau luând în considerare (5) și (1). scriem expresia (6): Deoarece mișcarea pendulului cu o sarcină este la fel de accelerată cu o viteză inițială egală cu zero, atunci la cel mai jos punct viteza sarcinii: unde a este accelerarea platformei cu sarcina, t 1 - timpul de coborâre a sarcinii. Din ecuațiile (9) și (10) putem exprima: Înlocuind valoarea vitezei liniare (11) în (12), obținem. Substituind în ecuația (4), valorile Mtr (8), v (11), (13), după transformare se obține o formulă de calcul pentru calcularea momentului de inerție al pendulului Oberbeck Rezultatele măsurătorilor și calculelor sunt prezentate în tabelul 1
unde este unghiul de rotație al pendulului atunci când sarcina se deplasează în jos cu o distanță h 1 și în sus cu h 2.
Deoarece firul este derulat de pe scripete în timpul alunecării, viteza liniară a punctelor situate pe suprafața scripetei este egală cu viteza sarcinii. Se știe că viteza unghiulară de rotație este legată de viteza liniară a mișcării unui punct de-a lungul circumferinței prin egalitate:
ORDINEA DE PERFORMANȚĂ
Articole similare