Derivarea tradițională a ecuației lui van der Waals
Starea unei anumite mase a oricărei substanțe poate fi descrisă cu ajutorul a trei parametri: presiunea \ (p \). din volumul \ (V \) și temperatura \ (T \). Acești parametri sunt interdependenți. Relația lor este descrisă de ecuația statului. care, în general, are forma: \ [F \ stânga (\ dreapta) = 0. \] O formă particulară a ecuației este dependentă de proprietățile substanței. De exemplu, un gaz diluat la o temperatură suficient de ridicată este bine descris de un model ideal de gaz. Ecuația de stare pentru aceasta este binecunoscuta ecuație Clapeyron (\ (1799-1864 \)). propusă în \ (1834 \) prin: \ [. pV = \ fracRT \] unde \ (m \) - masa gazelor, \ (M \) - masa molară (adică, greutatea unui mol de gaz) \ ( R \ este constanta universala a gazului. Pentru un mol de gaz, această ecuație are următoarea formă: [. PV = RT \] \ Efectuate mai târziu experimente a relevat deviere în comportamentul gazelor reale din legile gazelor ideale. Aceste rezultate au fost generalizate de fizicianul olandez Jan Diederik van der Waals (1837-1923). care în \ (1873) a propus o ecuație mai exactă a stării pentru un gaz real. Se numește ecuația lui van der Waals și, în calculul unei moli, este scrisă în forma \ [\ left>> \ right) \ left (\ right) = RT. \] Această ecuație ia în considerare forțele de atracție și repulsie care acționează între molecule. Forțele de atracție sunt luate în considerare datorită efectului de perete. Într-adevăr, pentru particulele din regiunea interioară, forțele atractive ale altor molecule sunt, în medie, compensate. Cu toate acestea, pentru particulele de lângă pereții vasului, o forță atractivă necompensată \ (f, \) este direcționată în vas. Această forță, pe de o parte, este proporțională cu concentrația particulelor (n \) din vas și, pe de altă parte, este proporțională cu concentrația particulelor din stratul de perete. Ca rezultat, obținem: \ (\ \ sim \ sim \ frac >>, \] unde \ (n \) este concentrația de molecule în vas, \ (V \) este volumul \ (1 \) gazului.
Efectul considerat de atragere a moleculelor din stratul de perete conduce la o scădere a presiunii asupra pereților vasului. În tranziție formală din ecuația Clapeyron ecuației Van der Waals, acest lucru corespunde înlocuirii \ [p \ la p + \ frac >>, \] unde \ (a \) - factor în funcție de gazul particular și dimensiunile vasului.
între moleculele de o forță de respingere într-un model al forțelor van der Waals sunt luate în considerare este foarte simplu: se presupune că moleculele au forma unei sfere de rază \ (r \) și nu se poate apropia unul de altul la o distanță între centrele de mai puțin \ (2r \.) Se poate presupune adică în jurul unuia dintre cele două molecule, există un "interzis" (pozitiv sau negativ), volumul (Figura \ (1 \)) egal \ [\ frac \ pi \ dreapta) ^ 3> = 8 \ cdot \ frac \ pi. \] Prin urmare, în calculul pentru o moleculă, volumul exclut este egal cu \ [= 4 \ cdot \ frac \ pi = 4, \] unde \ (\) este volumul unei molecule.
Ca rezultat. dacă în ecuația Clapeyron cantitate de spațiu disponibil pentru mișcarea de molecule este egal cu \ (V \) acum devine egal \ [V - = V - b, \] unde \ (\) - numărul Avogadro (egal cu numărul de molecule într-un singur mol de gaz), \ (b \) este volumul excluse datorită repulsiei moleculelor.

Fig.2 Jan Dideric Van der Waals
Presupunând că atracției și respingerii moleculare forțele acționează în comun și de înlocuire \ (p \) și \ (V \) expresii noi, obținem din ecuația Clapeyron van der Waals: \ [\ stânga (>> \ dreapta) \ stânga (\ dreapta) = RT. \]
Izotermele ecuației lui van der Waals
La o temperatură fixă, ecuația lui van der Waals descrie dependența lui \ (p \ left (V \ right).) În planul (pV) o astfel de dependență este reprezentată ca o familie de izoterme. fiecare dintre acestea corespunde unei anumite temperaturi. Pentru a investiga natura acestei dependențe, transformăm ecuația lui Van der Waals în următoarea formă: \ [>>> \ right] \ left (\ right) = RT \;> \ right | \ cdot,> \; \; + a> \ dreapta) \ stânga (\ dreapta) = RT,> \; \; + aV - pb - ab - RT = 0;>;; \; - \ stânga (\ dreapta) + aV - ab = 0 \;> \ right |: p,> \; \; - \ left (>> \ dreapta) + \ frac
V - \ frac>
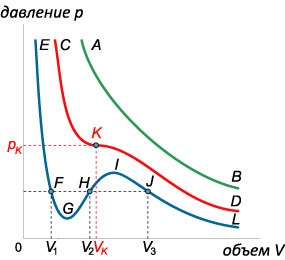
= 0.> \] Pentru o valoare fixă a lui \ (p1), ecuația rezultată este o ecuație de gradul trei în variabila \ (V \). Se știe că o ecuație cubică poate avea \ (1 \) sau \ (3 \) de rădăcini reale. Primul caz apare la temperaturile înalte \ (T \) (izotermul verde \ (AB \) din figura 1 (3 \)). Când temperatura este coborâtă, pe izotermă apare o secțiune ondulatoare. În acest caz, există trei rădăcini (izotermul albastru \ (EFGHIJL \)). Trecerea între două tipuri de izoterme are loc la o anumită temperatură \ (, \) care se numește temperatura critică.
> \ dreapta) + \ frac
V - \ frac>
= 0 \] ar trebui să fie scris ca \ [> \ dreapta) ^ 3> = 0. \] Extinderea diferență cub și egalează coeficienții de grade respective \ (V \) găsi expresiile pentru parametrii critici: \ [> \ dreapta) ^ 3 > = 0,> \; \; - 3 + 3 V - V_K ^ 3 = 0.> \] Presupunem că la punctul critic \ (p = \), \ (T = \.) Prin urmare, obținem: \ [- \ left (>
> \ right) = - 3 \\ \ frac >> = 3V_K ^ 2 \\ - \ frac >>> = - V_K ^ 3 \ end \ right.,> \; \; b + \ frac>
3 = \\ \ frac >> = 3V_K ^ 2 \\ \ frac >>> = V_K ^ 3 \ end \ dreapta ..> \] secțiune a treia ecuație a doua: \ [\ cere >> \ cdot \ anula >> = \ frac >>>>>,> \; \; . = 3b> \] defini \ Din a doua ecuație (: \). \ [= \ Frac >> = \ dreapta)> ^ 2 = >>>> >>> \] În cele din urmă, din prima ecuație ne găsim temperatură critică \ ( : \) \ [. = \ frac - b> \ dreapta) >>> = \ dreapta) \ cdot \ frac >>>>> = >>> \] Astfel, parametrii critici ai gazului în modelul van der Waals sunt dependente numai pe valorile \ (a, b \) și sunt definite de \ [= 3b,> \; \; \; = \ frac >>;>;; \; \; = \ frac >>.> \] Rețineți că am găsit valorile critice fără a utiliza derivatul. Se poate demonstra că în punctul critic cu parametrii \ (\) \ (\) \ (\) primul și al doilea derivat al funcției \ (p \ left (V \ dreapta) \) sunt egale cu zero (a se vedea exemplul \ (1 \) ).
Ecuația redusă de stare
Folosind parametrii critici ai \ (\) \ (\) și \ (\), puteți merge la variabilele adimensionale: \ [>>> \; \; \; >>> \, \, \; >>> \] și rescrieți ecuația lui van der Waals în forma redusă. \ [, \; P = \ pi, \; T = \ tau,> \; \; + \ Frac> \ dreapta)> ^ 2 >>>> \ dreapta) \ stânga (- b> \ dreapta) = R \ tau,> \; \; >>> + \ frac \ dreapta)> ^ 2 >> >> \ dreapta) \ stânga (\ dreapta) = R \ tau \ cdot \ frac >>,> \; \; >>> \ dreapta) \ stânga (\ dreapta) = 8 \ tau> \] Această ecuație este. mai universal decât ecuația inițială Van der Waals. Izotermele pentru diferite materiale, construite în conformitate cu ecuația de mai sus vor fi aceleași pentru aceleași valori \ (\ tau. \) Picioare organisme diferite, care sunt descrise de aceiași parametri dat \ (\ pi, \) \ (\ varphi, \) \ (\ tau, \) sunt numite stările corespunzătoare. În cazul în care oricare două dintre corp sau oricare două substanțe sunt date parametri identici, ei au aceeași magnitudine și o treime. Această proprietate universală este numită legea statelor corespondente. Să considerăm un alt interesant invariabil. Deoarece modelul van der Waals valori critice \ (\) \ (\) \ (\) pot fi exprimate doar prin cei doi parametri de \ (a \) și \ (b \) putem face o combinație a acestor valori, independente (b. \) de la \ (a \) și \ poate scrie următoarea relație: \ [>>>>> = >>>>>>>>> = \ cdot \ anula \ cancelR >> \ anula \ cdot 8 \ anulați >>> = >> \; \; \; \; \; \ ;. \ Frac >> >>> R = = 0,375> \] Acest raport se numește factor critic, și nu depinde de orice valori care caracterizează o substanță, adică, este o cantitate invariantă.Stadiile de tranziție de fază gaz-lichid și metastabile
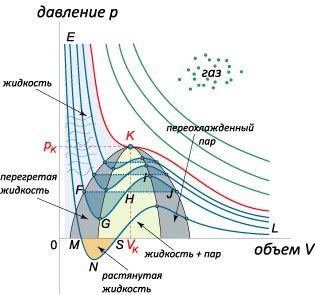
Considerăm din nou ecuația lui Van der Waals la temperaturi nu mai mari decât cele critice: \ (T 0, \) care corespunde unei stări instabile a materiei. La nivelul Fluctuația volumului \ (dV> 0 \) presiunea gazului va crește, de asemenea, (deoarece \ (dp> 0 \)), ceea ce duce la un gaz exploziv în expansiune. Pentru o fluctuație negativă, \ (dV 0 \)) se află în regiunea delimitată de spinodal. Zona diagramei între spinodal și binodal satisface practic criteriul de stabilitate \ (\ mare \ Frac >> \ normalsize 0.> \] Vedem că discriminant este întotdeauna pozitiv, adică, o ecuație pătratică are două rădăcini reale Ele sunt exprimate prin următoarea formulă :. \ [> = \ fracRT >>> \ dreapta) >>> = RT >>> RT> \ dreapta) >>> = RT >> \ dreapta) >> RT >>.> \] Prima rădăcină \ (\) cu semnul minus în numărătorul nu are nici o semnificație fizică, pentru că \ (0 \) parabole care corespunde numărătorul derivatului va fi direcționat peste ramuri. De aceea, derivatul își schimbă semnul de la minus la plus atunci când trece prin rădăcina dreaptă \ (\). Aceasta înseamnă că punctul \ (\) este minimul funcției \ (pV: \) (. => \) \
Astfel, atunci când gazul Rane Van der Waals este comprimat la o temperatură constantă, produsul \ (pV \) scade mai întâi, atingând valoarea minimă \ (\ dreapta) _>, \) și apoi începe să crească. Prima etapă se explică prin dominarea forțelor atractive între molecule, iar a doua etapă este asociată cu o creștere a contribuției forțelor repulsive.Unele gaze au temperaturi suficient de scăzute pentru Boyle. De exemplu, pentru helium \ (He \), acesta este \ (= 22.6 \; \ text, \) Pentru neon \ (Ne \), \ (= 122,1 \ temperaturile, astfel de gaze arată o dependență monotonă a \ (pV \) pe \ (v \)