Evident, nu există nici o limită a problemelor combinatoriale în care este necesar să se eticheteze marginile, vârfurile sau fețele diferitelor polihedra, astfel încât constantele magice să fie obținute în modul cel mai neașteptat. Multe dintre aceste probleme pot fi traduse într-o problemă echivalentă cu stelele magice. De exemplu, astfel. Care dintre cele cinci drepturi
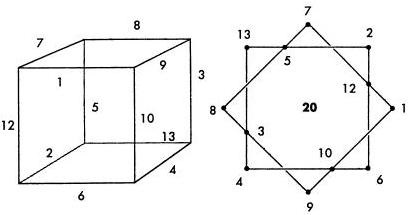
Acest număr nu este un număr întreg, deci nu merită să căutați un răspuns. Cu toate acestea, putem obține o decizie de defect (nu îndeplinește ultima condiție), cu constanta 20 cel mai puțin magic și cel mai mic număr maxim de 13 sunt marcate cu cercuri (și marginile echivalente ale cubului), așa cum se arată în figură.
Deoarece octoedrul este dual cubului, aceasta duce la soluția automată a problemei pe marginile etichetare octaedru diferite inconsistente nenule numere întregi pozitive, suma care în jurul fiecărei fețe dă constanta magică, iar cea mai mică.
După cum am văzut, fețele unui octaedru pot fi etichetate cu numere întregi consecutive, astfel încât vârfurile să devină magice. Pentru un icosaedron și un dodecaedru, constanța magică este fracționată, astfel încât să nu poată fi o soluție la problemă. Deoarece toate poliedre sunt două perechi, printre ele una care ar îndeplini condițiile impuse de probleme similare (întreg zero, fără număr de serie, dar cu fețe magice) nu există.
Materiale pe tema:
Trimiteți-le prietenilor:
Încercați să lucrați pentru:
Lucrări pe termen: