1. Găsiți inversul matricei:
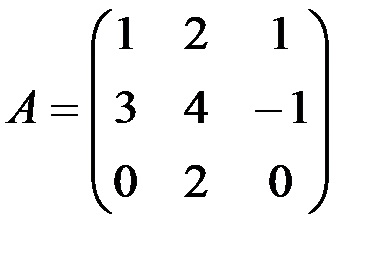
· Introduceți elementele matricei în intervalul celulelor A1: C3;
· Pentru a obține matricea inversă, selectați o gamă adiacentă de celule de aceeași mărime, de exemplu E1: G3 și introduceți formula matricei. Pentru a încheia formula în bretele curbate după introducerea formulei, apăsați CTRL + Shift + Enter.
2. Calculați factorul determinant al matricei A. Pentru aceasta, selectați orice celulă liberă, de exemplu A5, și introduceți formula
3. Calculați produsul matricei A cu matricea B, unde
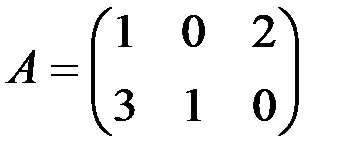
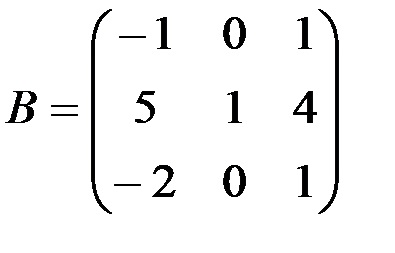
· Introduceți elementele matricei A în domeniul celulelor A10: C11;
· Introduceți elementele matricei B în domeniul celulelor A13: C15;
· Selectați o gamă de celule cu același număr de rânduri ca matricea A. și cu același număr de coloane ca și tabloul B. de exemplu, E10: G11 și introduceți formula
4. Rezolvați un sistem de ecuații liniare cu 3 necunoscute
metoda matricei inverse.
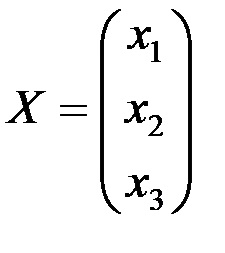
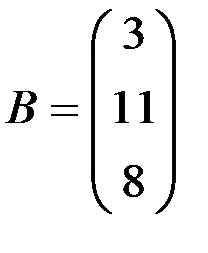
Soluția sistemului (1) în forma matricei are forma AX = B,
unde: A este matricea coeficienților;
X - coloana de necunoscuți;
B este coloana termenilor liberi.
Presupunând că matricea pătrată (2) a sistemului (1) nu este generată, adică determinantul său | A | ¹ 0, există o matrice inversă A. Apoi, metoda matrice-coloană X = A B va fi soluția sistemului prin metoda matricei inverse. Să găsim această soluție. Pentru a face acest lucru:
Să găsim determinantul | A | = 5 (vezi secțiunea 2). Pentru a face acest lucru, activați noua foaie de lucru și introduceți elementele matricei coeficienților A în intervalul celulelor A1: C3. Selectăm orice celulă liberă, de exemplu A5, și introducem formula
· Deoarece | A | 0 0, atunci matricea A este nondegenerată și există o matrice inversă A. Se găsește matricea inversă. Pentru a face acest lucru, selectăm gama necontinuă de celule de aceeași dimensiune ca matricea A. de exemplu E1: G3, și introduceți formula matricei.
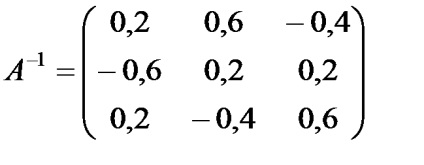
· Gasim solutia sistemului sub forma unei coloane matriceale
X = A B .. Pentru a face acest lucru, introducem elementele matricei B in gama celulelor E6: E8, selectam gama celulelor cu acelasi numar de randuri ca si matricea A. și cu același număr de coloane ca și tabloul B. de exemplu, G6: G8 și introduceți formula matricei
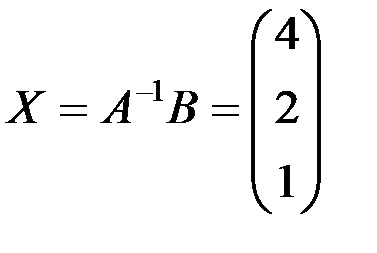
și anume soluția sistemului (4; 2; 1).