Tema 9. Modelarea soluției de ecuații în mediul de calcul tabelar MS Excel
Aflați cum să construiți modele matematice și să rezolvați ecuații în Excel.
De exemplu, se poate investiga modul în care rădăcinile unei ecuații patrate se schimbă în funcție de valorile coeficienților și de termenul liber.
Construim un model pentru rezolvarea ecuațiilor F (x) = 0 folosind metode tabulare, algebrice, grafice și numerice. Să investigăm dependența rădăcinilor ecuației de variația parametrilor funcției F (x).
Rădăcinile ecuației F (x) = 0 sunt punctele de intersecție a funcției F (x) cu axa X. De aceea, un grafic al unei funcții construite pe un anumit interval poate arăta imediat prezența rădăcinilor ecuației pe acest interval și valoarea lor numerică aproximativă.
Modelarea soluției de ecuații patratice ax 2 + bx + c = 0.
Pe o foaie mată Excel vom introduce notația parametrilor ecuației patratice a, b, c și discriminant D în celulele A2, B2, C2, D2.
Alocați numele celulei A3 A, B3 numele B, C3 numele C, D3 numele D cu comanda: Inserați - Nume - Alocați.
Introducem în aceste celule valorile parametrilor ecuației patratice. 1, 8, -2 în celulele A3, B3, C3 și formula pentru calculul discriminantului = B ^ 2-4 * A * C în celula D3.
Să analizăm dependența rădăcinilor de discriminatorii.
1. Metoda tabulară. Introduceți numărul de la -10 la 10 în pasul A în celulele A6: A26. În celula B6 se adaugă formula = A * A6 ^ 2 + B * A6-C și se multiplă până la B26. Să analizăm rezultatele obținute în tabel. Creați o copie a foii.
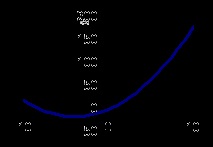
2. Metoda grafică. Selectați intervalul A5: B26 și porniți Expertul diagramă. În primul pas, selectați tipul graficului "Spot", vizualizați ca linie și faceți clic pe Terminare.
Să analizăm graficul rezultat al funcției și rădăcinile ecuației.
3. Metoda algebrică. Introducem formulele pentru calculul rădăcinilor cunoscute din matematică
din ecuația patratică: = (-B + ROOT (D)) / (2 * A) și = (-B-ROOT (D)
Soluția poate fi obținută cu un grad ridicat de acuratețe (în formate zecimale sau exponențiale)
4. Metoda numerică. Introducem în tabel valorile variabilei X la capetele intervalului 10 și -10 și la dreapta fundalului
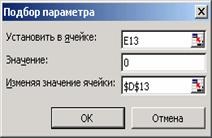
Setați cursorul pe celulă cu formula și executați comanda Instrumente - Selectare parametru. Să setăm valoarea 0 (F (X) = 0) în celula E13 prin schimbarea valorii celulei cu argumentul X. Astfel, rădăcinile ecuației F (X) = 0 vor fi aproximate aproximativ.
Realizăm operații similare în celula E14 și găsim a doua valoare numerică a rădăcinii ecuației. Cu o soluție numerică, Excel nu ne dă dreptul de a alege o metodă numerică, dar implementăm propria metodă integrată
Rezolvați ecuațiile: X 2 -4 = 0 și X 2 -X + 2 = 0.
5. Simularea soluțiilor de ecuații algebrice prin echipa Caută soluții
de exemplu, ecuațiile patratice ax 2 + bx + c = 0