Lucrul este, getComputedStyle (element) .getPropertyValue ("transform") returnează matricea (a, c, b, d, tx, ty). C traduce totul pare simplu: translateX = tx. translateY = ty. Iată cum să trageți scara, rotiți, oblic, nu înțeleg un pic, deoarece în primul rând în rotație și scară ar trebui să fie grade, în al doilea: ca skewX = b. skewY = c. și scaleX = a. scaleY = d. dar în același timp să rotim elementul în matricea a = cos (x). b = sin (x). c = -sin (x). dcos (x). În general, din setul de parametri matrice pe care l-aș fi construit, dar din parametrii de tragere a matricei nu înțeleg cum. Vă rog să-mi spuneți cum să traduceți matricea într-o limbă simplă înțeleasă de omul obișnuit sau să-mi spuneți cum puteți obține proprietatea de transformare nu în matrice. dar la scară. roti. traduce. oblic?
a fost văzută ultima dată pe 8 decembrie 15 la 19:55
Proiectul de specificație descrie ce înseamnă valorile.
Transformările se realizează folosind o matrice de transformare, în general (3D) o matrice de 4x4
Matricea pe care o obțineți matricea (a, c, b, d, tx, ty) este reprezentată după cum urmează:
După cum ați observat în mod corect: tx, ty - responsabil pentru mișcare.
Scalarea corespunde valorilor situate pe diagonala principală, în cazul nostru este a, d. La el a - scalarea pe lățime, d - înălțime.
c, b - responsabil pentru panta
și toate împreună a, b, c, d - pentru o întoarcere.
Mai multe detalii pot fi văzute în imagine
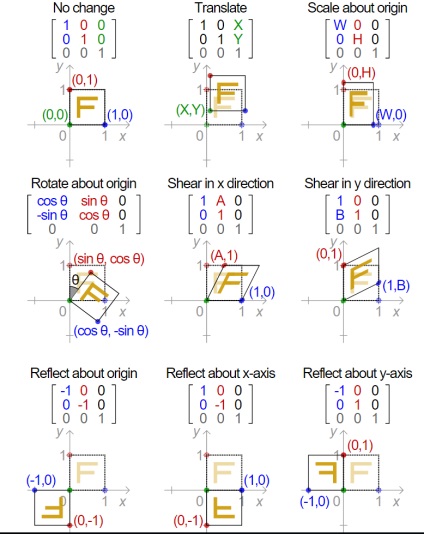
@ Kirpich643, de fapt, dacă sunt aplicate mai multe transformări care definesc lor foarte non-triviale, deoarece transformările reprezintă un plus de matrice-vector sau matrice, și din moment ce avem doar două stări: o inițiale - de fapt matricea de identitate și finite - este foarte problematică cunoașterea vectorului pe care se înmulțește matricea - Grundy Dec 9 '15 la 6:13 am