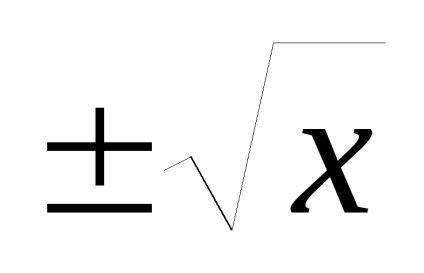Așa cum am menționat deja, pentru funcția uniformă y = f (x), relația f (x) = f (-x) este valabilă în întregul domeniu al variației argumentului său. În consecință, o funcție de acest fel are aceleași valori pentru toate valorile argumentului, egale în valoare absolută, dar opuse în semn. Graficul unei funcții uniforme este simetric cu privire la axa ordinelor.
Pentru a construi graficul unei funcții uniforme y = f (x), este necesar să construim o ramificație a graficului acestei funcții numai în regiunea valorilor pozitive ale argumentului x
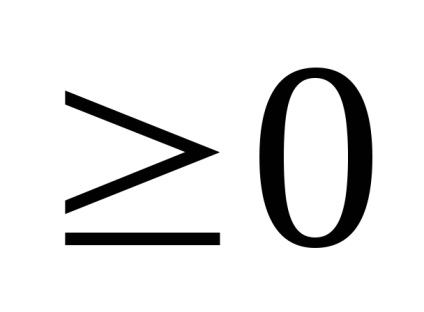
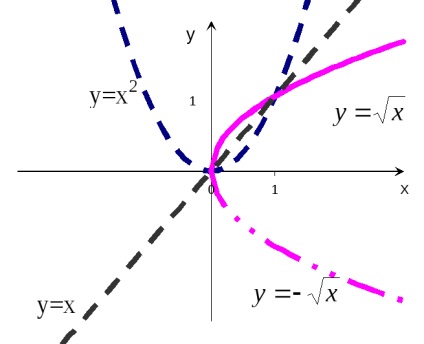
Exemplul 8. Construiește un grafic al funcției y =
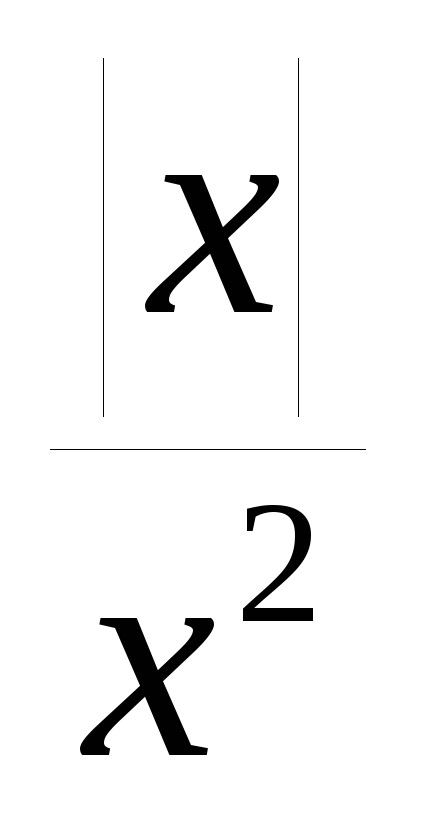
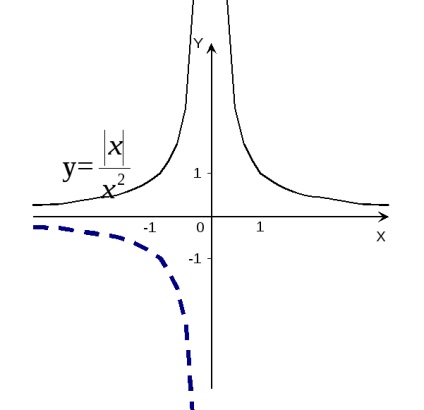
R eference: Această funcție este uniformă, deci este suficient să construim graficul numai în regiunea valorilor pozitive ale lui x (punctul x = 0 nu este inclus în domeniul definiției funcției). Pentru x> 0, funcția originală are forma y =

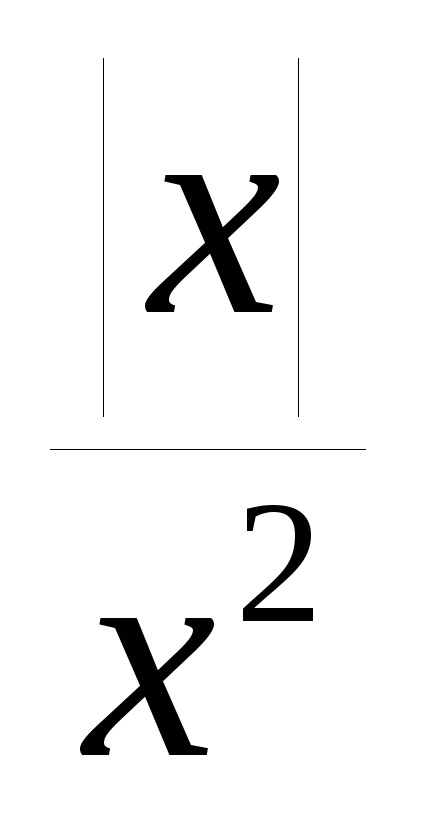
Pentru o funcție ciudată y = f (x), egalitatea f (-x) = -f (x) se află în intervalul tuturor valorilor argumentului. Astfel, în regiunea valorilor negative ale argumentului, ordonatele grafului unei funcții ciudate sunt egale în magnitudine, dar opuse în semn de ordinul graficului aceleiași funcții pentru valorile pozitive corespunzătoare x. Graficul unei funcții ciudate este simetric în raport cu originea.
Pentru a construi graficul unei funcții ciudate y = f (x), este necesar să construim o ramificație a graficului acestei funcții numai în regiunea valorilor pozitive ale argumentului (x
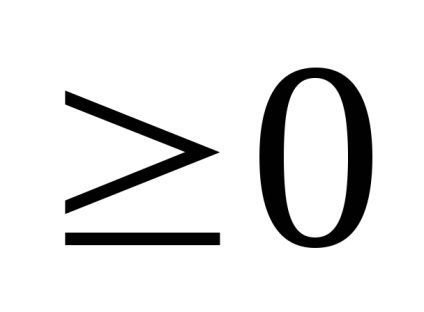
Graful y = f (x) în regiunea valorilor negative ale argumentului este simetric construit ramură în raport cu originea și pot fi obținute prin reflectarea ramurilor în raport cu axa ordonatei, urmată de o reflecție în regiunea valori negative ale lui x în raport cu abscisa.
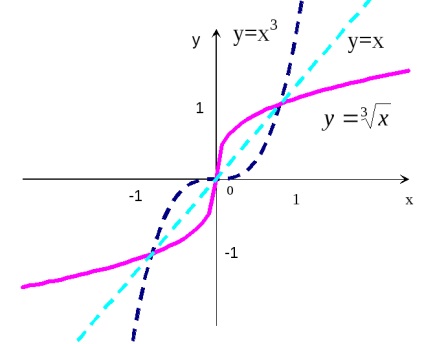
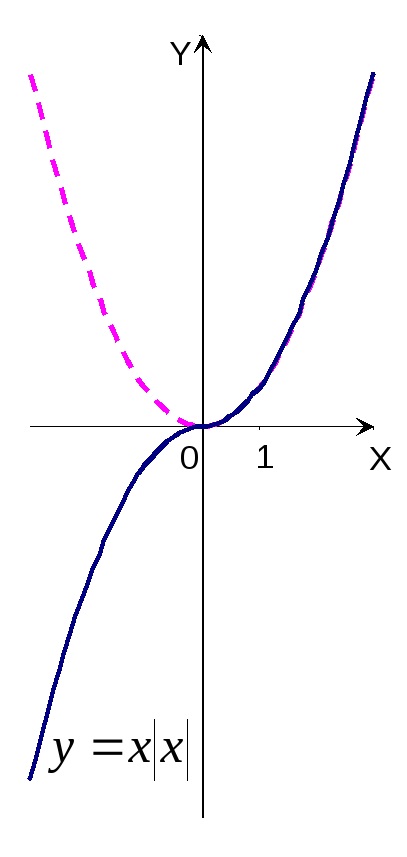
Exemplul 9. Construiește un grafic al funcției y = x

R eference: Funcția inițială este ciudată, așa că o construim în regiunea valorilor pozitive ale argumentului (x
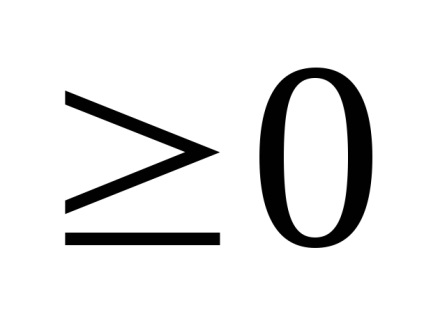

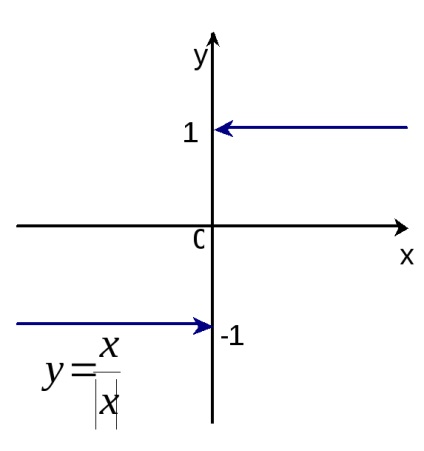
Exemplul 10. Construiește un grafic al funcției y =
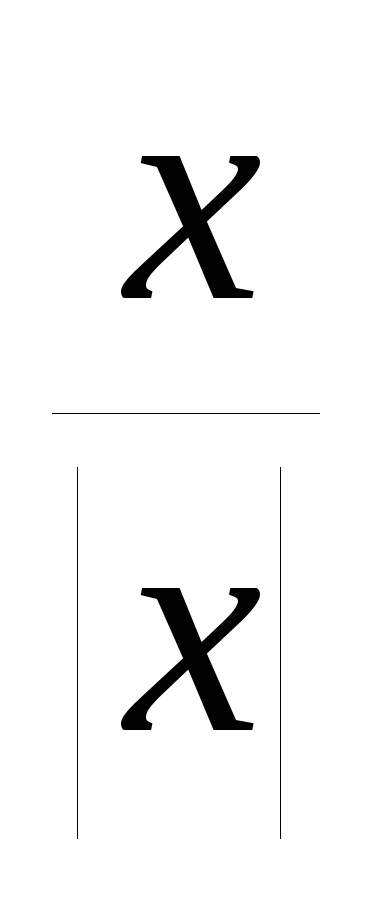
R eference: Această funcție este ciudată, așa că vom construi graficul numai în regiunea x> 0 (punctul x = 0 nu se află în domeniul definiției funcției), unde are forma y = 1. Ramura graficului acestei funcții pentru x<0 получаем отражением относительно начала координат построенной ветви кривой (рис.13). Стрелки означают, что точки (0,1) и (0,-1) не принадлежат графику.
2.4. Construcția graficului funcției inverse
Funcțiile directe și inverse exprimă aceeași relație între variabilele x și y, cu singura diferență că în funcția inversă a acestor variabile sunt schimbate peste, care este echivalentă cu schimbarea axelor denumiri. Prin urmare, graficul funcției inverse este simetrice funcții grafice directe bisector relativă

Pentru a construi un grafic al funcției y =
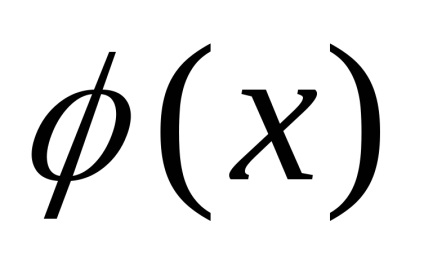
Exemplul 11. Construiește un grafic al funcției y =

Remediu: H