Metoda 1 Soluție utilizând formula pentru rezolvarea ecuației patrate
Verificați dacă ecuația cubică dată dvs. are un termen independent. După cum sa menționat mai sus, ecuațiile cubice sunt de forma ax 3 + bx 2 + cx + d = 0, unde coeficienții „b“, „c“ și „d“ poate fi egal cu 0, adică ecuația cubică poate fi compus dintr-un singur membru (i variabilă în gradul al treilea). Mai întâi, verificați dacă ecuația cubică dată are un termen liber, adică "d". Dacă există un membru gratuit, puteți rezolva această ecuație cubică, folosind formula pentru rezolvarea unei ecuații pătratică.- Dacă există un membru disponibil, utilizați o altă metodă de soluție (vedeți secțiunile următoare).
- Un exemplu. 3x 3 + -2x 2 + 14x = 0. Dacă puneți "x" în paranteze, veți obține x (3x 2 + -2x + 14) = 0.
- Acest lucru este adevărat, deoarece orice număr sau expresie, înmulțit cu 0 este 0. Deci, ai scos „x“ din paranteze, vă întindeți o ecuație cubică în doi factori ( „x“ și o ecuație de gradul doi), dintre care unul trebuie să fie egale 0, astfel încât întreaga ecuație este 0.
Metoda 2 Găsirea soluțiilor integrale prin factoring
Verificați dacă ecuația cubică dată dvs. are un termen independent. Metoda descrisă în secțiunea anterioară nu este potrivită pentru rezolvarea ecuațiilor cubice în care este prezent un termen liber. În acest caz, va trebui să utilizați metoda descrisă în această secțiune sau în secțiunile următoare.- Un exemplu. 2x 3 + 9x 2 + 13x = -6. Aici transferați termenul liber d = -6 în partea stângă a ecuației pentru a obține 0: 2x 3 + 9x 2 + 13x + 6 = 0 pe partea dreaptă.
- În exemplul nostru, a = 2 și d = 6. Multiplicatorii 2 sunt numerele 1 și 2. Factorii 6 sunt numerele 1, 2, 3 și 6.
- În exemplul nostru, împărțiți multiplicatorii "a" (1, 2) cu factorii "d" (1, 2, 3, 6) și obțineți: 1, 1/2, 1/3, 1/6, 2, 2/3. Acum adăugați la acest rând de numere valorile lor negative: 1, -1, 1/2, -1/2, 1/3, -1/3, 1/6, -1/6, 2, -2, 2/3 , -2/3. Soluțiile complete ale ecuației cubice date sunt în această serie de numere.
- Divizarea conform schemei Horner nu este un subiect ușor; Pentru mai multe informații, faceți clic pe linkul de mai sus. Iată un exemplu de găsire a uneia dintre soluțiile ecuației cubice date prin diviziunea lui Horner: -1 | 2 9 13 6 __ | -2-7-6 __ | 2 7 6 0 Deoarece restul este 0, una dintre soluțiile ecuației este un întreg -1.
Metoda 3 Utilizarea discernământului
În această metodă veți lucra cu valorile coeficienților "a", "b", "c", "d". Prin urmare, este mai bine să scrieți în prealabil valorile acestor coeficienți.- Un exemplu. x 3 - 3x 2 + 3x - 1. Aici a = 1, b = -3, c = 3, d = -1. Nu uitati ca atunci cand nu exista un coeficient inainte de "x", inseamna ca coeficientul este 1.
- În exemplul nostru: b 2 - 3ac (-3) 2 - 3 (1) (3) 9-3 (1) (3) 9 - 9 = 0 = Δ0
- În exemplul nostru, Δ0 = 0 și Δ1 = 0, găsirea lui Δ nu este dificilă. Δ12 - 4Δ03) ÷ -27a 2 (0) 2 - 4 (0) 3) ÷ -27 (1) 2 0 - 0 ÷ 27 0 = Δ, prin urmare ecuația dată are una sau două soluții.
- În exemplul nostru: 3 √ ((Δ12 - 4Δ03) + Δ1) / 2) 3√ (√ ((02 - 4 (0) 3) + (0) 0) + (0)) / 2) 0 = C
- Dacă înlocuiți valorile corespunzătoare ale cantităților din această formulă, veți obține soluțiile posibile ale ecuației cubice care vi se oferă. Înlocuiți-le în ecuația inițială și dacă egalitatea este îndeplinită, atunci soluțiile sunt corecte. De exemplu, dacă puneți 1 în 1, puneți 1 în x 3 - 3 x 2 + 3x - 1 și obțineți 0. Aceasta înseamnă că egalitatea este respectată și 1 este una dintre soluțiile ecuației cubice date.
Această pagină a fost vizualizată de 77,746 ori.
Soluția online de probleme, ecuații, inegalități ITservice
Rezolvarea soluțiilor online de ecuații logaritmice
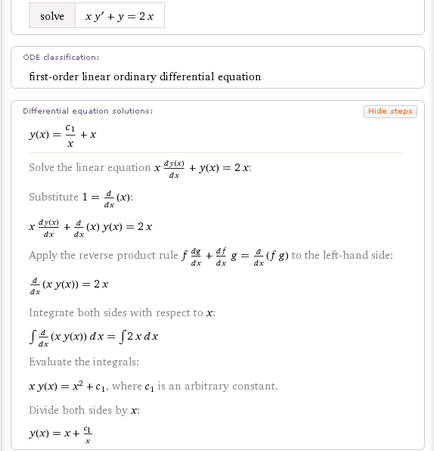
Cum se rezolvă ecuațiile cubice
Ecuații diferențiale online

Rezolvarea problemelor online!
Ecuațiile online - t


Mai mult de 25 de idei cele mai bune pe tema "Decorați-vă de casă"
TOATE FABRICELE Magazin online Cumpara en-gros tesaturi sau in

Modelul unui rucsac - lecții de tăiere și

Masina de tricotat Design si operare