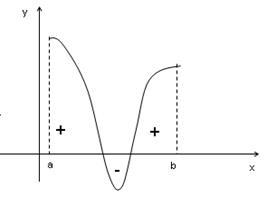
Se știe că un integral integrat pe un interval este aria trapezului curbilinar mărginit de graficul funcției f (x). Dacă graficul este sub axa Ox, adică f (x) <0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x)> 0, atunci zona are semnul "+".
Formula este utilizată pentru a găsi suprafața totală.
Un exemplu. Găsiți zona unei figuri mărginită de linii
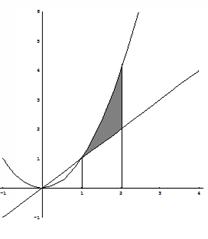
Zona dorită (umbrită în figură) poate fi găsită din formula:
Dacă trapezoidul curbilinar este limitat de o curbă dată parametric
. linii drepte x = a, x = b și axa Ox, atunci suprafața sa este dată de formula
unde # 945; și # 946; sunt determinate din egalitatea x (x, 0,) = a și x (# 946;) = b.
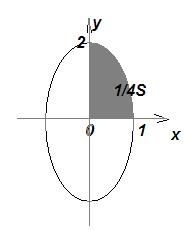
Un exemplu. Calculați aria figurului delimitată de elipsă x = cost, y = 2sint.
Mai întâi găsim ¼ din suprafața S. Aici x variază de la 0 la 1, deci t variază de la π / 2 la 0. Se constată:
Un exemplu. Găsiți zona unei figuri delimitată de o curbă dată parametric :.
Să aflăm ce formă este limitată de curba dată. Funcțiile x = x (t) și y = y (t) sunt definite, continue și diferențiate pentru orice valoare reală a parametrului. În cazul în care. atunci. dar dacă. . atunci.
Cea mai mare valoare a lui x durează pentru x '(t) = 0, 2-2t = 0; t = 1, x (1) = 1; y (1) = 1. Dacă x = 0, atunci t = 2 sau t = 0. Pentru aceleași valori ale parametrului y = 0. Astfel punctul cu coordonatele (0; 0) este un punct de auto-intersecție. În consecință, aria necesară este limitată de o buclă a curbei situată în primul cvadrant și corespunde unei modificări a parametrului de la t = 0 la t = 2 cu o direcție by-pass pozitivă.
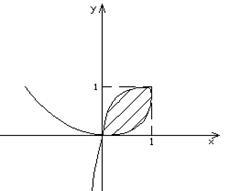
Zona figura dorită poate fi calculată din formula
Deoarece unele curbe pot fi date prin ecuații parametrice simple, este adesea mai convenabil să se calculeze suprafața unei figuri delimitată de o curbă închisă în coordonate carteziene prin accesarea formei parametrice a înregistrării.