Torsiunea barelor cilindrice.
Luați în considerare o bară cilindrică (fig.1), ale cărei suprafețe laterale sunt libere de tensiuni și momente direcționate de-a lungul liniei axiale a tijei sunt aplicate pe suprafețele de capăt. Axa este direcționată de-a lungul axei tijei.
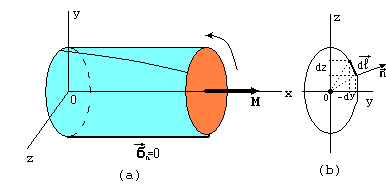
Fig.1 Torsiunea tijei în momentul respectiv. Pe suprafața laterală, forțele nu acționează: vectorul de stres este zero.
Folosim ecuațiile de echilibru al unui mediu elastic în absența forțelor de masă:
Ecuațiile (1) trebuie rezolvate cu condiții omogene (vector de stres egal cu zero) la suprafața laterală, unde vectorul normal
Pe fața frontală, vectorul principal de forță trebuie să fie zero, iar momentul principal este dat și are o componentă numai pe axă. Prin urmare, pentru componentele vectorului principal, obținem
pentru componentele momentului principal avem condiția vectorului
sau trei scalari
Presupunem că secțiunile normale ale tijei rămân plate și se rotesc doar într-un unghi proporțional cu distanța dintre ele
Deformările și stresurile non-verde sunt:
Observăm că tensiunile îndeplinesc în mod identic ecuațiile de echilibru (1) și ultimele două condiții limită (1) și substituția lor în prima condiție (2) dă relația
unde este un punct arbitrar pe suprafața laterală a cilindrului.
Condiția (6) poate fi îndeplinită identic numai dacă presupunem că secțiunea transversală a cilindrului este un cerc.
Condițiile (3) ale dispariției vectorului principal de forță
Sunt mulțumiți dacă axa trece prin centrul de greutate al secțiunii.
Condițiile (4) pentru momentele de la capătul cilindrului ia forma
Astfel, pentru o tijă cu secțiune transversală circulară, este posibil să se construiască soluția complet, deoarece unghiul de întoarcere este determinat de prima condiție din (7):
unde momentul geometric al inerției secțiunii față de axă
În cazul general, atunci când secțiunea transversală nu este un cerc, planul său de torsiune este distorsionat, deci vom căuta o soluție pentru deplasări sub forma
Apoi, deformările și solicitările nonzero sunt după cum urmează:
Condițiile de echilibru (1) conduc la ecuația funcției
Apoi condițiile (2) pentru absența forțelor pe suprafața laterală sunt echivalente cu ecuația pentru punctele de contur ale secțiunii
Luând în considerare faptul că pentru un punct arbitrar al conturului
noi rescriem condiția (11) în formular
Astfel, ținând cont de ecuația (10), definiția funcției de torsiune se reduce la rezolvarea problemei lui Neumann. Pentru o funcție conjugată cu o funcție armonică
. și anume condițiile Cauchy-Riemann sunt îndeplinite, obținem din (12)
Adică, problema lui Dirichlet a fost obținută. Constanta de integrare pentru cazul contururilor multiplicate ale unei secțiuni pe fiecare contur își asumă valoarea.
Dacă introducem funcția de stres, obținem
Funcția de stres satisface ecuația Poisson
cu condiție limită
pe fiecare dintre contururile secțiunii în cazul multitudinii sale.
Să verificăm condiția ca vectorul principal al forțelor aplicate la capetele tijei să fie egal cu zero. deoarece,
Să găsim momentul forțelor la capătul tijei
unde aria delimitată de conturul limitei zonei de secțiune multiplă conectată și pentru conturul exterior a pentru celelalte contururi, constantele sunt determinate din starea de continuitate a vectorului de deplasare atunci când traversează conturul.
Atunci când se calculează integrala peste contururile interioare ale limitei, se ia în considerare faptul că traversarea conturului părăsește regiunea pe partea stângă și, de asemenea, că
unde aria zonei este limitată de un contur.
Pentru un circuit simplu conectat
pentru un circuit multiplu conectat
Teorema privind circulația stresului la forfecare. Determinarea constantelor pentru o secțiune multiplă conectată a conturului.
Teorema privind circulația forței de forfecare de-a lungul oricărui contur închis:
I =. în cazul în care zona delimitată de contur
În calculul circulației, luăm în considerare formulele (8) pentru deplasare
și formulele (9) pentru solicitări
Ca urmare a înlocuirii stresului în expresia pentru circulație, obținem:
Deoarece în virtutea neclarității deplasării pentru traversarea conturului, integrala
Aplicând teorema circulației la fiecare contur interior al limitei unui domeniu multiplu conectat, obținem un sistem de ecuații pentru determinarea
Să verificăm rezultatele obținute cu exemplul unui contur delimitat de două cercuri concentrice de rază exterioară și rază interioară.
Condiția egalității la zero pe suprafața exterioară poate fi îndeplinită dacă căutăm funcția de stres în formă
După înlocuirea în ecuația Poisson, obținem
Aplicăm teorema circulației la conturul interior
Astfel, această funcție de stres satisface toate condițiile problemei.
Să găsim momentul de acțiune prin calcul direct și folosind formula (17):
Torsionarea unui cilindru cu o secțiune eliptică
Luați în considerare un cilindru al cărui contur al secțiunii este o elipsă.
Vom căuta funcția de stres în formă
care este, evident, zero pe contur. Operatorul său Laplace este
de unde găsim Sonstantu B
Stresul maxim tangențial este atins la limită și este egal cu
Calculând momentul, găsim raportul său cu unghiul de torsiune
Torsionarea unei tije de secțiune transversală dreptunghiulară.
Luați în considerare torsiunea unei bare de secțiune dreptunghiulară:
Vom căuta funcția de stres sub forma unei serii
Cu această extindere pe limite, înlocuim (20) în ecuația Poisson
Înmulțiți laturile stângi și drepte ale egalității prin integrarea cu w, luând în considerare ortogonalitatea funcțiilor u, adică
Calculul (22) după integrare conduce la următoarele ecuații pentru funcțiile:
O soluție satisfăcătoare
Astfel, funcția de stres se găsește sub forma unei serii:
Găsim soluția într-un alt mod. Luați în considerare un dreptunghi în care. Apoi, având în vedere condițiile de graniță, putem căuta o soluție în formă
În (24), funcția va satisface ecuația armonică. Dacă, ca și mai înainte, problema este rezolvată prin metoda de separare a variabilelor, pentru funcțiile obținute obținem ecuații omogene
Deoarece avem nevoie de soluții chiar și noi
Să găsim constantele din condiție. Pentru a face acest lucru, multiplicăm ecuația
și integrați de la.
Ca rezultat, obținem:
Diferența dintre soluția (25) și (23) este esențială, deoarece o parte a seriei este însumată, iar seria rămasă converge rapid.
Dacă găsim momentul și stresul maxim de forfecare, obținem:
Pentru profilele sub formă de benzi subțiri de lățime și lungime
și pentru profile deschise compuse din mai multe benzi
Torsiunea unei tije cu pereți subțiri cu secțiune multiplă conectată.
Lăsați ca secțiunea transversală a tijei să fie o regiune multiplă conectată cu pereți subțiri (figura 2). Vom presupune că grosimea este mult mai mică decât raza de curbură
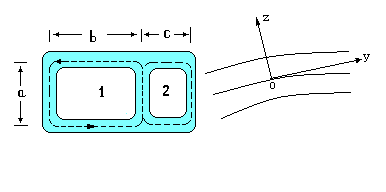
Fig. 2 Tija cu perete subțire cu secțiune multiplă conectată
Apoi, pentru elementul selectat, peretele peretelui peretelui poate fi considerat paralel și soluția depinde slab de variabila. În acest caz, ecuația Poisson poate fi aproximată în formă
Soluția ecuației (26), ținând cont de condițiile limită, dă funcția de stres
În cadrul acestei aproximări Deoarece cantitatea este mică, al doilea termen poate fi neglijat, iar tensiunea de forfecare poate fi considerată ca o valoare constantă
Aplicăm teorema asupra circulației tensiunii tangențiale la fiecare contur (există două asemenea circuite în figura 2). În acest caz, pe conturul exterior, vom presupune că constantul este zero, pe conturul 1 vom presupune că este egal, iar pe conturul 2 egal cu
Rezolvarea sistemului obtinut cu privire la constante, gasim
Dacă se presupune că grosimea este aceeași, formulele sunt simplificate