Așteptarea (valoarea medie) a procesului stochastic X (t) se numește funcția nealeatorii timpului mx (t), a cărei valoare la fiecare punct în timp egal cu media secțiunii proces aleatoriu corespunzător
În acest caz, mx (t) reprezintă, ca atare, axa simetriei realizărilor individuale, adică gradul de dispersie față de axa medie.
Pentru procese staționare
Pentru procesele ergodice
Pătratul mediu al procesului aleatoriu X (t) caracterizează puterea medie a procesului și se determină prin formula:
Pentru procese staționare
Pentru procesele ergodice
Varianța procesului aleatoriu X (t) este funcția temporală non-aleatoare Dx (t), a cărei valoare la fiecare instant este egală cu variația secțiunii corespunzătoare a procesului aleator
Pentru procese staționare
Pentru procesele ergodice
Asteptarile matematice si varianta caracterizeaza procesul in sectiuni separate, dar nu iau in considerare relatiile lor, aceasta relatie se caracterizeaza printr-o functie de corelare.
Corelația (autocorelare) aleatoare X (t) de proces este numit Rxx (t1, t2) Argumentul două funcții non-aleatoare, care, pentru fiecare pereche de valori ale t1 și t2 este argumente egale de timp corelare secțiuni proces aleatoriu corespunzător
Funcția de corelare caracterizează gradul de interrelație statistică dintre două secțiuni ale unui proces aleatoriu.
Funcția de corelare este
Funcția de corelare mutuală caracterizează gradul de interrelație statistică între secțiunile transversale pentru două procese.
Pentru procesele aleatoare Gauss, caracteristica definitorie este o densitate de probabilitate bidimensională și, prin urmare, funcția de corelare caracterizează complet proprietățile statistice ale procesului aleatoriu.
Pentru procesele staționare, funcția de corelare depinde de diferența dintre argumentele = t2-t1
Varianța este
Pentru procesele ergodice
Proprietățile de bază ale funcției de corelare
1. Valoarea inițială a funcției de corelare este egală cu variația
2. Valoarea Rx () pentru orice nu poate depăși valoarea inițială
3. Funcția de corelare este simetrică în raport cu argumentele sale
Pentru funcțiile corelate reciproc, acest lucru nu este adevărat
4. Funcția de corelare a proceselor staționare este o funcție uniformă, iar funcția de corelație este o funcție ciudată
5. Funcția de corelare a sumei Z (t) = X (t) + Y (t), unde X (t) și Y (t)
6. Funcția de corelație a produsului Z (t) = X (t) Y (t), unde X (t) este un proces aleator și Y (t) este o interferență non-aleatoare
7. Funcția de corelare a sumei Z (t) = X (t) + Y (t), unde X (t) este un proces aleator și Y (t) este o funcție nonrandom
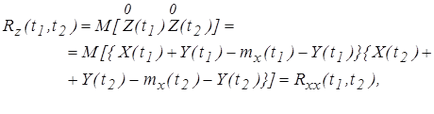
8. Pentru funcția de autocorelare, putem scrie expresie
Pentru funcția de corelare, putem scrie expresie