Scopul lucrării este de a studia pendulul lui Maxwell și de a determina cu el momentul inerției solide.
Bazele teoretice ale lucrărilor de laborator
În această lucrare de laborator, momentul inerției solide este determinat experimental cu ajutorul pendulului lui Maxwell.
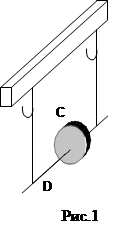
Momentul de inerție a corpului este o măsură a inerției corpului în cursul mișcării de rotație. Momentul inerției corpului depinde de mărimea și forma corpurilor și de distribuția masei corporale față de axa de rotație.
Momentul inerției corpului este o cantitate aditivă. Dacă cineva își imaginează un corp format dintr-un număr mare de elemente foarte mici Dmi. atunci momentul de inerție al unui astfel de corp discret este aproximativ determinat de formula
Cu cât este mai precis, cu atât este mai mare numărul de partiții ale corpului în masele elementare Dmi.
Pentru o valoare infinit de mare a numărului de mase elementare, am tendința de infinit și Dmi. tinde la zero. Apoi momentul de inerție al unui solid solid (distribuția continuă a masei) este determinat de formula
unde ri este distanța de la element la axa de rotație; r este densitatea materiei în elementul de volum dV, situat la o distanță r de axa de rotație.
Astfel, problema găsirii momentului de inerție a diferitelor corpuri se reduce la integrarea conform formulei (1) pentru volumul corespunzător al corpului.
În derivarea formulelor computaționale, relațiile sunt folosite pentru momentele de inerție a corpurilor și legea conservării energiei mecanice totale.
Având în vedere că momentul de inerție al unei valori a cuplului aditiv a corpului, valoarea teoretică a pendulului inerțial Maxwell Jt poate fi determinată ca suma momentelor de inerție obținute ca urmare a integrării prin formula (1) pentru cele trei elemente: un inel cu axa pendulului de antrenare și ca purtat de un disc
momentul inerției axei pendulului;
moment de inerție a discului
momentul inerției inelului pus pe disc;
Energia cinetică a unui pendul de masă m ridicată și fixată la o înălțime h. este egal cu zero. Energia mecanică totală este determinată numai de energia potențială E n = mgh.
În poziția inferioară a pendulului, En = 0 și energia mecanică totală este egală cu suma energiilor cinetice ale mișcărilor de translație și rotație
Cu această mișcare, modulul de viteză unghiulară w. modulul de viteză liniară u și raza discului R sunt legate de
Din legea conservării rezultă că energia totală a pendulului în pozițiile superioare și inferioare ar trebui să fie aceeași, adică
Prin urmare, luând în considerare relația (4), momentul inerției pendulului
Pentru mișcarea equiconverge, relația dintre distanța h. traversat de corp, viteza u și timpul t au forma
Înlocuind ultima expresie din formula (6), obținem dependența pentru determinarea valorii experimentale a momentului de inerție
Ecuația (8) poate fi de asemenea derivată pe baza ecuațiilor dinamice pentru mișcarea de translație și rotație (a se vedea Lab 5).
Vederea generală a plantei este prezentată în Fig. Baza 1 este o coloană fixă cu cronometru electronic 2 la care este fixat un suport fix superioară 9 și brațul inferior mobil 7. superior Brațul 10 este un electromagnet, iar senzorul fotoelectric 11, iar pedalierul - senzor fotoelectronice 3.
Pendulul este un disc 5 fixat pe axa 6 suspendată pe două toroane 4 (suspensie bifilară). Pe disc, puteți pune inelele de schimb 12, schimbând astfel momentul inerției sistemului.
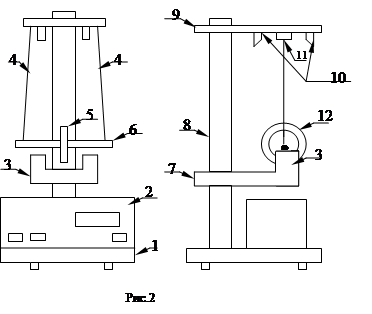
Pendulul este reținut în poziția sa superioară de un electromagnet 10. Senzori optici 3 și 11 sunt conectate cu un cronometru electronic 2. superior senzor electronic detectează începutul pendulului și inferior - mișcarea de închidere (coborâre) a pendulului.
Ordinea de executare a muncii
- Puneți una din inelele pe discul pendulului.
- Activați instalarea făcând clic pe butonul "rețea".
- Setați axa pendulului într-o poziție orizontală.
- Coborâți capătul inferior al pendulului la aproximativ 2 mm sub axa optică a senzorului fotoelectric. (Pendulul este reglat prin modificarea lungimii firului sau deplasarea consolei inferioare la înălțimea dorită.)
- Porniți electromagnetul (butonul "Start" trebuie să fie în poziția apăsată).
- Virați firul de suspensie uniform pe axa pendulului până când pendulul este blocat cu un electromagnet în poziția superioară.
- Măsurați timpul de cadere al pendulului cu cronometrul electronic apăsând butonul "Resetare" și apoi "Pornire".
8. Repetați pașii 1-7 de zece ori.