Creșteți și scădeți intervalele funcției
Pentru a găsi intervalele la care funcția crește sau scade. Se utilizează adesea o metodă bazată pe analiza semnelor derivate ale funcției respective. Esența acestei metode este după cum urmează.
Dacă funcția y = f (x) crește strict pe interval (a, b) și are un derivat la fiecare punct x0 al intervalului. apoi, așa cum se arată în figura 1, precum și în figura 2,
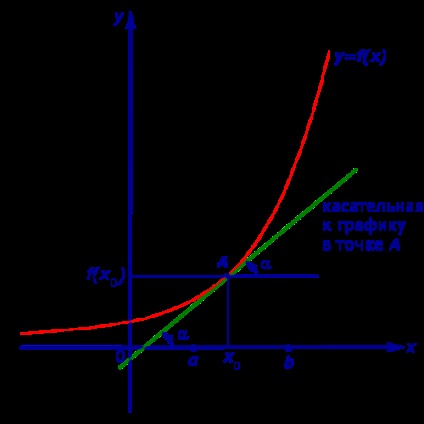
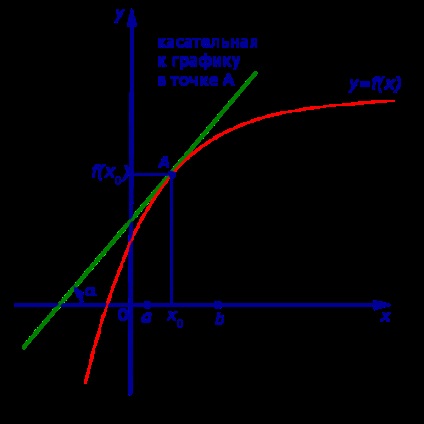
Unghiul α al pantei tangentei în graficul funcției este acut, ceea ce implică inegalitatea:
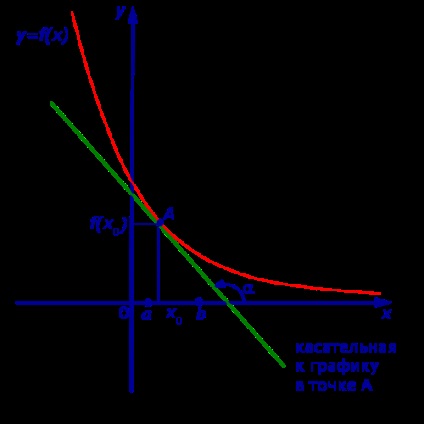
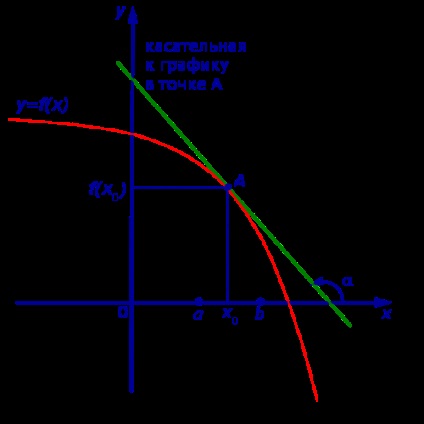
Unghiul α al pantei tangentei în graficul funcției va fi grav, de unde urmează inegalitatea:
Condiții suficiente pentru creșterea și scăderea funcției
În următoarea afirmație, a cărei dovadă depășește cursul școlar al matematicii, sunt formulate suficiente condiții pentru creșterea și scăderea funcției.
a). Dacă la fiecare punct x al intervalului (a, b) derivatul f '(x) există și satisface inegalitatea
b). Dacă la fiecare punct x al intervalului (a, b) derivatul f '(x) există și satisface inegalitatea
c). Dacă la fiecare punct x al intervalului (a, b) derivatul f '(x) există și satisface inegalitatea
g). Dacă la fiecare punct x al intervalului (a, b) derivatul f '(x) există și satisface inegalitatea
Extreme (maxime și minime) ale funcției
Definiție 1. Punctul x0 se numește punctul maxim al funcției f (x). dacă există un interval (a, b). astfel încât un 3 + 3x 2 |
Pe de altă parte, din moment ce soluția inegalității
Prin definiția modulului. egalitatea
Din această ecuație rezultă că, dacă reflectăm simetric pe axa Ox relative ale y1 funcției graficului = x 3 + 3x 2 (Fig. 10), situată în jumătatea inferioară, lăsând o parte neschimbată a acestui grafic, care se află în jumătatea superioară, obținem graficul y = | x 3 + 3x 2 | (Fig.11).
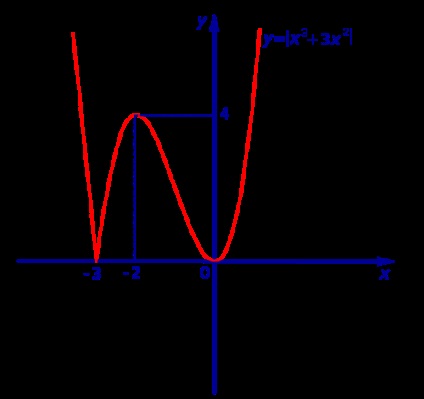
La punctul x = - 3, derivatul funcției y = | x 3 + 3x 2 | nu există. În toate celelalte puncte ale axei numerice derivatul funcției y = | x 3 + 3x 2 | acolo.
Pe site-ul nostru puteți să vă familiarizați și cu materialele de instruire elaborate de profesorii Centrului de Resolvent pentru pregătirea pentru USE în domeniul matematicii.
Pentru elevii care doresc să se pregătească bine și să treacă examenul pentru matematică, fizică sau rusă la un scor mare, centrul de formare "Resolventa" conduce