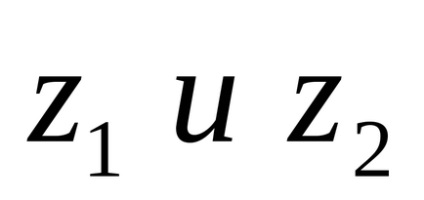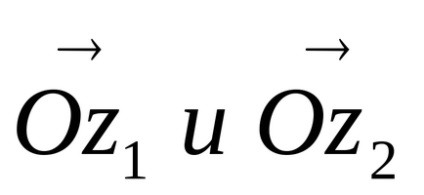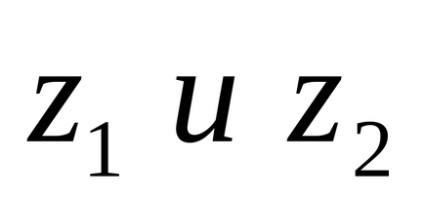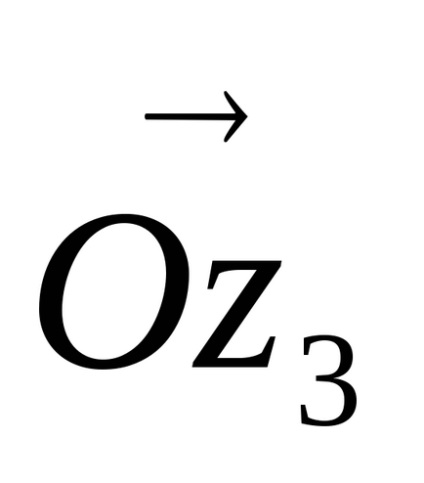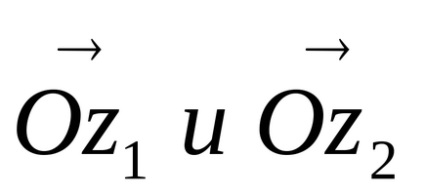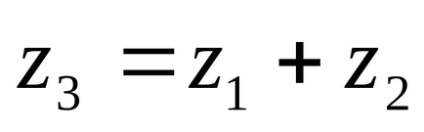Numărul complex z este simbolul x + yi, unde x și y sunt numere reale. Aici x este numit partea reală a numărului complex, y este partea imaginară, eu este unitatea imaginară.
Partea reală a numărului complex este desemnată ReZ (ReZ = x), iar partea imaginară este notată cu simbolul ImZ (ImZ = y). În consecință, se poate scrie un număr complex.
Înregistrarea unui număr complex
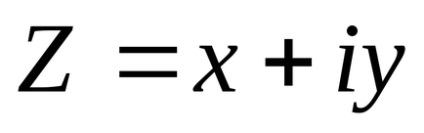
Numărul complex
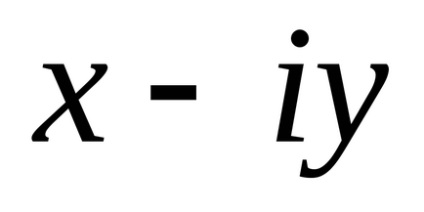
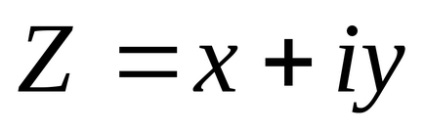
Numere complexe
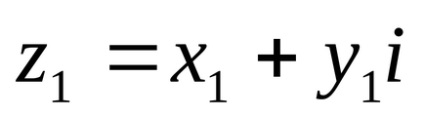
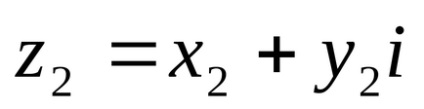
Dacă y = 0, atunci numărul complex are forma
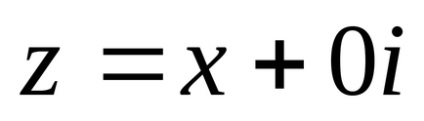
Dacă x = 0, y ≠ 0, atunci numărul complex are forma z = 0 + yi sau, pe scurt, z = yi. Se numește un număr imaginar. În special, dacă x = 0, y = 1, obținem un număr complex
0 + 1i = i este o unitate imaginară. Fiecare număr z = x + yi, unde y ≠ 0, se numește un număr imaginar.
Cele două numere complexe x + yi și x-yi se numesc conjugate complexe. Dacă z = x + yi, atunci conjugatul x-yi este de obicei indicat prin
Operațiuni cu numere complexe.
Suma numerelor complexe se numeste numarul complex. Este notat cu
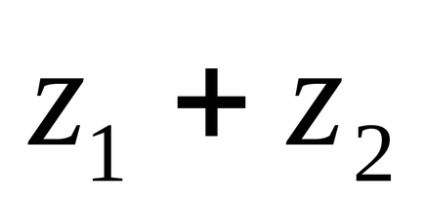
Când se adaugă numere complexe, se adaugă părțile lor reale și imaginare.
Numărul complex
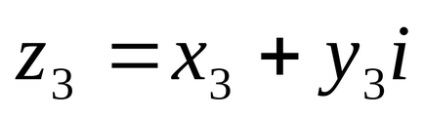
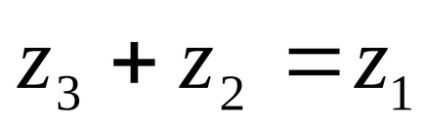
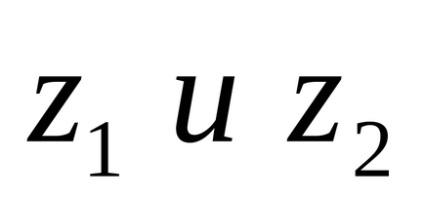
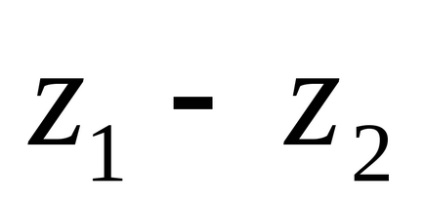
Din definiție rezultă că
Când se scade din părțile reale și imaginare ale părții reduse, părțile actuale și imaginare ale subtradei sunt scăzute în mod corespunzător.
Înmulțirea a două numere complexe este introdusă de către
Egalitatea (4) rezultă din
Dacă multiplicați două numere complexe
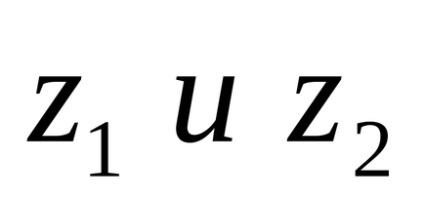
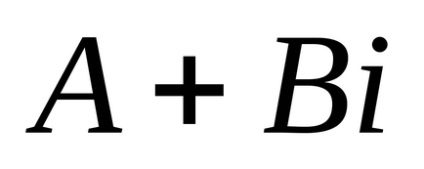
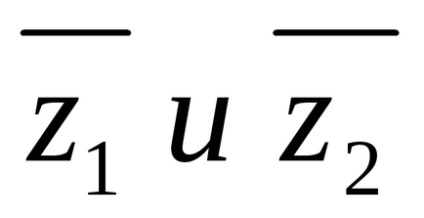
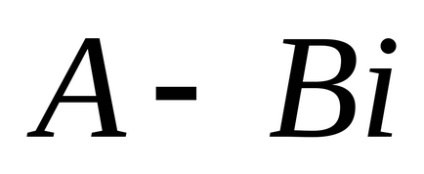
Diviziunea este introdusă ca un invers de înmulțire. Un coeficient al unui număr este un număr
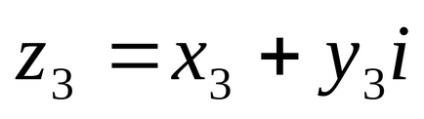
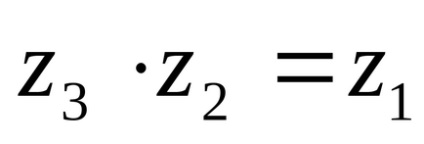
Prin urmare, pe baza egalității (4), obținem:
Rezolvarea sistemului (7) cu privire la
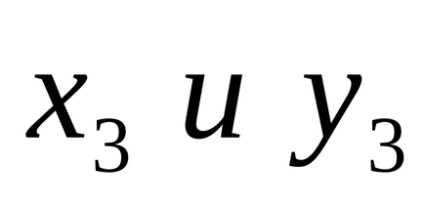
(în cazul în care
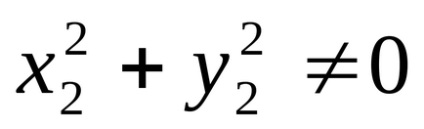
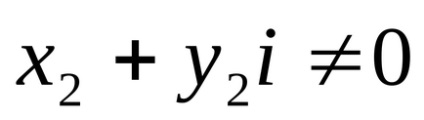
Este ușor de observat că egalitatea (9) poate fi obținută prin înmulțirea numărătorului și a numitorului fracțiunii
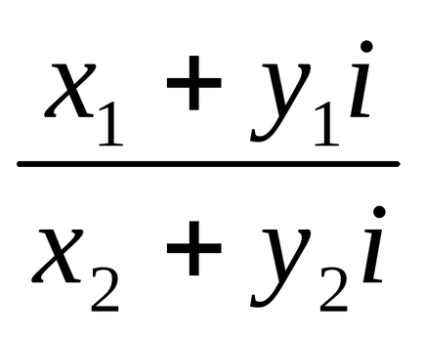
Construcția unui număr complex z într-o putere naturală a n este considerată ca un caz special de multiplicare a numerelor complexe:
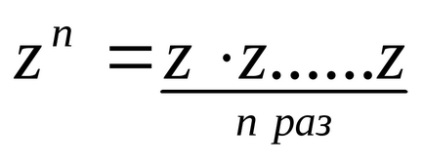
Numerele complexe pot fi considerate o extensie a setului de numere reale. De fapt, operațiile algebrice pe numere complexe sunt introduse astfel încât colectarea tuturor numerelor complexe "reale" (adică numerele formei
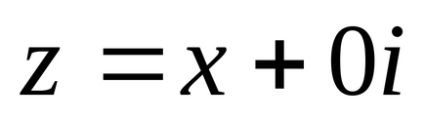
z = x cu operațiunile indicate pe acestea coincide cu colectarea de numere reale și acțiuni cunoscute pe aceste numere.
Forma trigonometrică a unui număr complex. Alegem sistemul de coordonate polare de pe planul XOY (Figura 1), astfel încât polul să coincidă cu originea, iar axa polare să meargă de-a lungul direcției pozitive a axei reale. Indicați raza polară a punctului
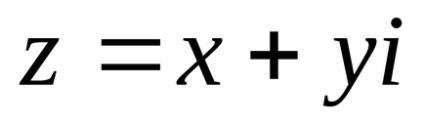
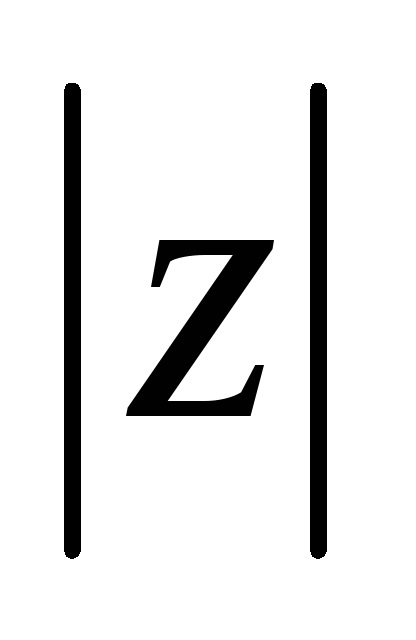
,
unde k este un număr întreg arbitrar și φ este oricare dintre valorile argumentului z. Deoarece, a
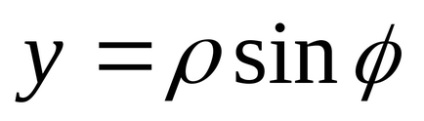
(*)
Expresia (*) se numește forma trigonometrică a numărului complex. Este evident că
Interpretarea geometrică a adăugării de numere complexe. Lăsați avioanele unei variabile complexe să primească două numere
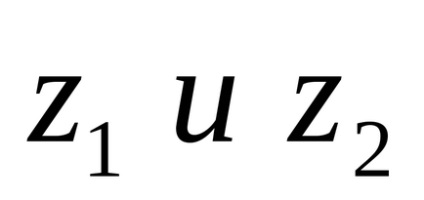
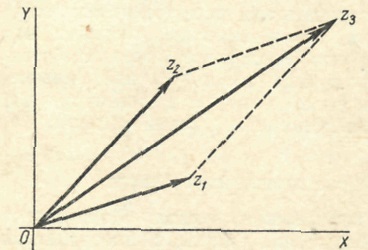
Desenarea vectorilor de rază ai punctelor