DOMENIUL DE ENERGIE ELECTRICĂ.
3.1 Distribuția sarcinilor pe conductor.
Încărcările electrice comunicate conductorului din exterior sunt distribuite într-o stare de echilibru, astfel încât câmpul electric din interiorul conductorului este absent
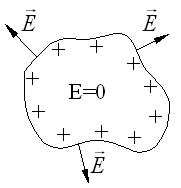
Astfel, în condiții de echilibru al încărcării, atât suprafața cât și volumul conductorului sunt echipotențiali.
Dacă încărcăturile sunt în echilibru, atunci în orice punct al conductorului vectorul este perpendicular pe suprafață, adică u = 0. Într-adevăr, dacă ≠ 0. atunci aceasta ar cauza mișcarea sarcinilor de-a lungul suprafeței conductorului și nu ar exista nici un echilibru.
Se poate demonstra teoretic și se verifică experimental că densitatea de suprafață a sarcinilor la punctele individuale ale conductorului crește cu atât mai mult curbura suprafeței. Luați în considerare un model simplu. Fie ca două raze r1, care sunt suficient de îndepărtate unul față de celălalt, să fie separate unul de celălalt. și r2 sunt conectate printr-un fir subțire (Figura 41). Dacă una dintre bile are o anumită încărcare, se va întinde pe suprafața exterioară a bilelor și a conductorului, astfel încât potențialele bilelor să fie egale. Deoarece bilele sunt îndepărtate suficient și câmpul firului poate fi neglijat, potențialul bilelor poate fi calculat din formula:
care rezultă din relația dintre tensiune și potențial.
Dar curbura suprafeței, atunci.
În cazul unui conductor de formă arbitrară, fiecare element al suprafeței sale poate fi considerat ca o secțiune a unei suprafețe sferice cu o anumită curbură. Concluzia rezultată poate fi extinsă la o primă aproximare în acest caz.
Să vedem cum forța câmpului de lângă suprafața unui conductor încărcat este legată de densitatea de suprafață a încărcărilor de pe acesta. Aplicăm teorema Gauss. Deoarece este perpendiculară pe suprafața conductorului, alegem ca suprafață Gaussian un cilindru drept, o înălțime dh și o zonă de bază dS,
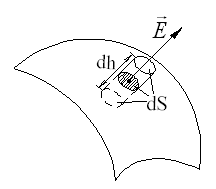
, și de atunci, ajungem
σ. Deoarece densitatea sarcinii de suprafață σ este mai mare în cazul în care curbura suprafeței este mai mare, rezistența lui E este maximă în apropierea marginilor și proeminențelor ascuțite ale conductorului.
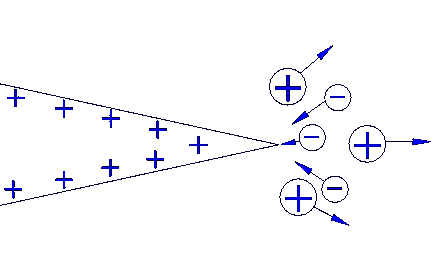
Câmpul electric în astfel de locuri poate fi atât de puternic încât se dovedește a fi capabil să ionizeze moleculele de aer. Există un fenomen numit debitul de sarcină de la conductor.
Ionii de aer care se formează intră în mișcare. Ioniunile cu același semn ca și încărcătura vârfului se mișcă din punct, purtând împreună cu ele molecule neutre
3.2 Conductorul într-un câmp electric extern.
Taxele incarcate, spre deosebire de legaturile, pot fi scoase din conductor si separate unul de celalalt.
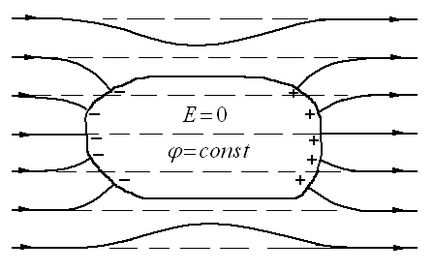
Tensiunile induse pot provoca redistribuirea sarcinilor care creează un câmp extern și distorsionarea câmpului extern. 45a prezintă liniile de câmp ale unei sfere încărcate uniform, în Fig. 45b este distorsiunea liniilor de forță care au apărut atunci când un conductor suplimentar neîncărcat a fost introdus în câmpul sferei.
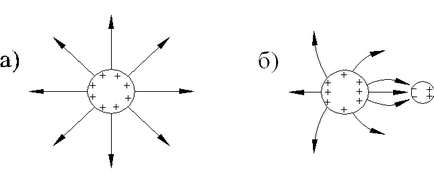
Câmpul electric din interiorul conductorului este absent, indiferent dacă conductorul solid sau cavitatea, deoarece încărcăturile induse sunt amplasate numai pe suprafața exterioară a conductorului. Aceasta este baza protecției electrostatice. Atunci când un dispozitiv trebuie protejat de câmpuri externe, el este înconjurat de un ecran conductiv. Câmpul extern este compensat în interiorul ecranului de încărcăturile induse de pe suprafața acestuia.
Capacitatea electrică a conductorilor.
Între încărcarea unui conducător solitar și potențialul său există o relație proporțională
capacitate electrică conductor izolat - cantitatea scalară fizică ce caracterizează conductorul capacitatea de a acumula sarcină electrică și numeric egală cu valoarea taxei care trebuie să fie raportate conductor neîncărcată la potențialul a devenit egal cu unitatea, cu condiția ca toate celelalte organism eliminate pe termen nelimitat și că potențialul punctului infinit la distanță presupune a fi zero.
Capacitatea electrică a unui conductor solitar depinde de forma și dimensiunile conductorului, de permitivitatea dielectrică a mediului înconjurător. Nu depinde de materialul conductorului, temperatura, starea agregatului, dimensiunile și forma cavităților interne, sarcina și potențialul.
Pentru a calcula capacitatea unui conductor, este necesar să se calculeze potențialul datorat încărcării conductorului. De exemplu, într-o minge solitară de rază r plasată într-un mediu infinit omogen, cu o permitivitate dielectrică ε, apare un potențial φ atunci când sarcina q îi este împărțită.
Deoarece și.
3.4. Capacitate electrică reciprocă. Condensator.
Conductorii solitari au o capacitate mică și nu sunt capabili să acumuleze încărcături electrice apreciabile. Dacă conductorul nu este izolat, atunci capacitatea acestuia depinde de aranjamentul relativ al corpurilor care înconjoară conductorul. Acumulările induse pe corpuri slăbesc câmpul creat de sarcina q în locul unde este localizat conductorul. Ca rezultat, potențialul conductorului scade, iar capacitatea crește. Efectul este amplificat în special dacă conductorul încărcat este abordat de corpuri încărcate cu o sarcină diferită a conductorului.
Prin aranjarea corectă a conductorilor și umplerea spațiului între ele cu dielectrici cu o constantă dielectrică ridicată, puteți concentra sarcini semnificative pe conductori.
Capacitatea electrică reciprocă a doi conductori este o cantitate numerică egală cu valoarea absolută a sarcinii care trebuie transferată de la un conductor la altul astfel încât valoarea absolută a diferenței de potențial dintre ele să devină unitate:
Că capacitatea electrică reciprocă a conductorilor nu depinde de organele din jur, este necesar ca câmpul electric creat de conductorul taxe a fost concentrat numai între conductoare. Acest lucru se realizează prin aceea că conductorii sunt formate fie din două plăci paralele, aflate la distanțe mici sau doi cilindri coaxiali sau sfere concentrice și le raportează egale în mărime și în semn opus tarifelor. Un astfel de sistem de conductori se numește condensator. Conductoarele care formează condensatorul sunt numite plăci. Valoarea absolută a sarcinii unei plăci este numită încărcarea condensatorului.
Capacitatea electrică a unui condensator este o cantitate fizică care este numeric egală cu raportul dintre sarcina condensatorului și valoarea absolută a diferenței de potențial dintre plăcile sale:
Capacitatea unui condensator depinde de forma, dimensiunile, poziția relativă a plăcilor, permitivitatea dielectrică a dielectricului dintre plăci.
Să derivăm formula de capacitate pentru un condensator plat (figura 46). Fie S o zonă a unei fețe, distanța dintre plăci,
Să găsim diferența potențială dintre plăci, folosind legătura dintre rezistența și potențialul câmpului electrostatic în formă integrală.
Dar sarcina condensatorului este.