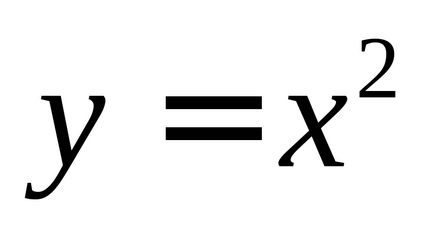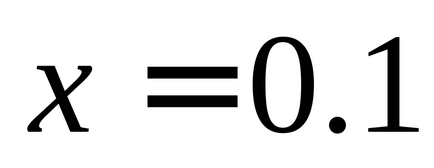LUCRAREA LABORATORULUI nr. 7-1
DEZVOLTAREA GEOMETRICĂ A DERIVATIVULUI
Derivatul unei funcții continue este una dintre caracteristicile sale cele mai importante. Este folosit în sarcina de a studia comportamentul unei funcții, construirea graficului său, în probleme de optimizare condiționată și necondiționată și multe altele. Derivatul unei funcții continue a unei variabile la un anumit punct x este definit ca limita raportului dintre creșterile sale și incrementarea argumentului, deoarece acesta din urmă tinde la zero:
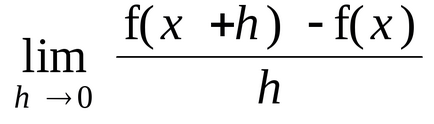
Pentru a calcula derivatele din Maple, există o comandă specială diff (), care vă permite să calculați atât derivatele oricăror ordine de funcții ale unei variabile, cât și derivatele parțiale ale funcțiilor mai multor variabile.
Semnificația geometrică a derivatului. Tangent la graficul de funcții
Începem cu demonstrarea semnificației geometrice a derivatului ca tangent al unghiului de înclinare a tangentei la graficul funcției la un anumit punct. Tangenta este definită ca poziția limitativă a secantului care trece prin două puncte ale graficului atunci când una dintre ele tinde către cealaltă. Construim toate construcțiile utilizând exemplul unei funcții:
Vom calcula derivatul la punctul x0 = 1. Pentru aceasta, definim funcția și două puncte ale graficului cu abscise, respectiv x0 = 1 și x1 = x0 + h:
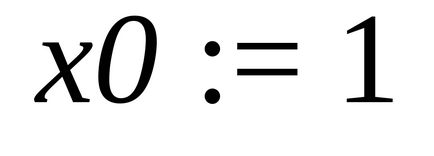
Panta de comandă () (panta) din pachetul student calculează tangenta pantei dreptei care trece prin două puncte date:
> cu (student): t: = pantă (p0, p1);
Acum, dacă h este setat la zero, atunci expresia t trebuie să se converge la un număr egal cu tangenta unghiului de înclinare al secantului în poziția limită, adică tangentă a unghiului pantă al tangentei la graficul funcției la punctul x = 1. Setați secvența valorilor h_values convergând la zero:
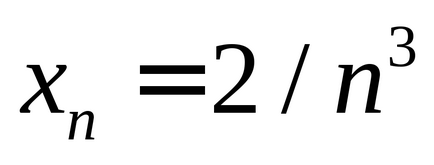
> seq (evalf (t), h = valori);
-5,439033250, -12,57034624, -13,3498521, -13,5137879, -13,569058,
-13,592932, -13,604946, -13,611648, -13,615686, -13,61826,
Se poate observa că această secvență converge și foarte rapid. Dar converge la valoarea derivatului unei funcții la punctul x = 1? Calculăm derivatul cu funcția diff ():
Comanda eval este folosită pentru a înlocui valorile numerice cu o funcție. Comanda evalf este utilizată pentru a calcula valoarea aproximativă a unei expresii.
Observăm că secvența construită de noi converge la valoarea derivatului la punctul x = 1. Deja membru al cincisprezecelea are două semne exacte după punct zecimal. Rezultatul exact se obține dacă se calculează limita expresiei t pentru h 0:
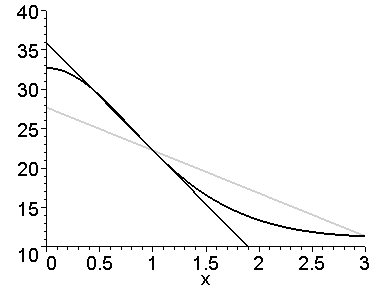
Capabilitățile grafice ale Maple vă permit să vedeți cum se apropie secantul de tangenta. Construi ecuație ca linie secantă care trece prin cele două puncte obținute după coordonatele (x0, y (x0)) și (x0 + h, y (x0 + h)), respectiv (unde Y este X variabilele dependente și independente):
Exprimăm variabila dependentă Y în termeni independenți X și o reprezentăm sub forma unei funcții:
Comanda neaplicată convertește o expresie într-o funcție. Comanda rhs înseamnă "partea dreaptă" - partea dreaptă a expresiei. % indică rezultatul operațiunii anterioare. Am obținut ecuația secantă.
În mod similar, construim o ecuație tangentă sub forma unei funcții. Ecuația cunoscută a tangentei este utilizată aici.
Acum putem construi o secvență de imagini care să conțină graficul funcției, tangenta și secantul acesteia la schimbarea parametrului h și afișarea acesteia sub forma unei animații cu comanda display ():
> S: = seq (plotare ([y (x), linie_tang (x), linie_sec (x)],
vedere = [0..3,10..40], culoare = [negru, negru, verde], grosime = 2),
> cu (parcele): afișare (S, insequence = true);
ASSIGNMENT 1. Rezolvați aceleași probleme specificând alte secvențe h_values Secant va tinde spre o tangență mai lentă dacă
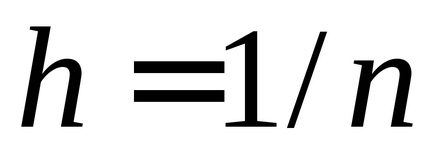
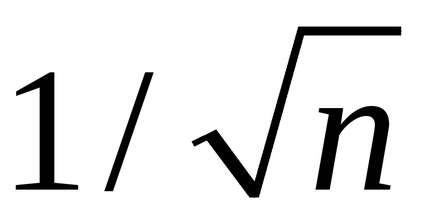
Sarcina 2. Investigați aproximarea secantului la tangenta funcției