Vectorul vitezei unui punct la un anumit moment al timpului este egal cu primul derivat al vectorului său de rază în raport cu timpul. Vectorul de viteză este tangent la traiectoria punctului dat în direcția mișcării.
Punctul de accelerare în forma vectorială.
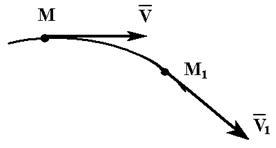
Lăsați punctul să se deplaseze pe o traiectorie curbilină. La momentul respectiv
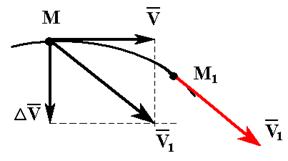
Transferăm vectorul paralel cu el însuși la punctul M și construim un paralelogram cu o latură și o diagonală. Apoi, evident, cealaltă parte este DV.
Raportul creșterii vectorului de viteză cu intervalul de timp pentru care a apărut această creștere este numit vectorul de accelerație mediu. Direcția este aceeași ca și.
Accelerarea la un moment dat este egală cu limita
Dacă punctul se deplasează de-a lungul unei traiectorii rectilinii, atunci vectorul de accelerație este îndreptat de-a lungul acestei linii drepte.
Dacă punctul se deplasează de-a lungul unei traiectorii curbilinii (plan), atunci vectorul de accelerație este îndreptat spre concavitatea curbei.
1.2. Metoda coordonată pentru specificarea mișcării unui punct.
Poziția unui punct în spațiu și pe o traiectorie este determinată în mod unic de cele trei coordonate x, y, z.
Când punctul se mișcă, coordonatele vor varia în funcție de timp.
y = f2 (t) este legea mișcării punctului
z = f3 (t) în forma coordonată.
Determinați traiectoria unui punct.
Dacă t este considerat ca parametru în ecuațiile care exprimă legea mișcării, atunci aceste ecuații vor reprezenta ecuațiile traiectoriei în formă parametrică. Pentru a obține ecuația traiectoriei în forma coordonată, trebuie să eliminăm parametrul t.
Determinarea vitezei unui punct în metoda coordonate a postului
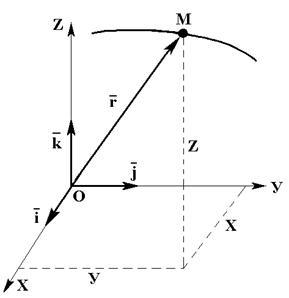
este determinată de vectorul de rază
sau trei coordonate carteziene.
Coordonatele pot fi considerate ca
proiecția unui vector de rază dat
axe. Construim vectorii unitari da-
Se descompune vectorul de rază de-a lungul axelor de coordonate: