Complexitatea proceselor computaționale este un concept al teoriei de complexitate a calculelor. estimați resursele (de obicei timpul) necesare pentru a efectua algoritmul.
definiție
Fie A un algoritm pentru rezolvarea unei anumite categorii de probleme și o dimensiune a unei probleme individuale a acestei clase. poate fi, de exemplu, dimensiunea matricei care este procesată. numărul de vârfuri ale graficului procesat. Denumim funcția, dă limita superioară a numărului maxim de operații de bază (adunare, multiplicare etc.) pe care trebuie să le îndeplinească algoritmul A, rezolvând problema dimensională. Spunem că algoritmul A este polinomial. dacă nu crește mai repede decât un polinom de. În caz contrar, A este un algoritm exponențial.
Se pare că între aceste clase de algoritmi este o diferență semnificativă: dimensiunea mare a problemei (care este de obicei cel mai interesant în practică), algoritmi polinomiali pot fi efectuate pe computerele moderne, în timp ce algoritmii exponențiale pentru dimensiunea practică a problemei, de regulă, nu se poate să fie pe deplin îndeplinite. De obicei, rezolvarea problemelor, generarea de algoritmi exponențiale asociate cu o listă completă a tuturor opțiunilor, și având în vedere imposibilitatea practică de a implementa o astfel de strategii pentru rezolvarea lor a dezvoltat o abordare diferită.
De exemplu, chiar dacă există un algoritm exponențial pentru găsirea soluției optime a unor probleme în practică aplicarea altor algoritmi polinomiali mai eficiente pentru constatare nu este neapărat cel mai bun, dar numai o soluție acceptabilă (aproximativ optimului). Dar chiar dacă problema are o soluție cu ajutorul unui algoritm polinomial, acesta poate fi construit numai după o înțelegere profundă a esenței problemei.
Polimomiali algoritmii pot varia, de asemenea, în mod semnificativ, în funcție de gradul de polinomul care aproximează dependența. Luați în considerare estimările complexității în timp a algoritmului. O astfel de evaluare este realizată folosind relația ("Big O"): ei spun că ea crește ca și pentru N mare și este scrisă ca. Dacă există o constantă constantă Const> 0, astfel încât. Apoi, estimarea lui O (g (N)) se numește complexitatea de timp asimptotică a algoritmului.
Evaluarea (g (N)) funcție este utilizată atunci când valoarea exactă nu este cunoscută, și cunoscută procedura pentru creșterea timpului petrecut pe decizia dimensiunii problemei N folosind algoritmul A. Valorile exacte depind de punerea în aplicare specifice, în timp ce O (g (N) ) este o caracteristică a algoritmului în sine. De exemplu, în cazul în care complexitatea asimptotic timp a algoritmului este (Un astfel de algoritm se numește pătratică), apoi cu creșterea N prin rezolvarea problemei crește cu pătratul N. Faptul că algoritmul de complexitate exponențială în termeni de simboluri introduse pot fi scrise ca. Unde k este de obicei un număr mai mare decât unul.
Un alt tip de evaluare este asociat cu introducerea de "mici în": spun că nu crește mai repede pentru N mare, este înregistrat. În cazul în care. De exemplu, este evident că. Un alt exemplu: algoritmul A este polinomul dacă. Unde P k (N) este un polinom în N de grad k. Astfel, un algoritm al cărui complexitate asimptotică este egală cu (N log N) se referă la cele polinomiale.
Exemple de complexități asimptotice
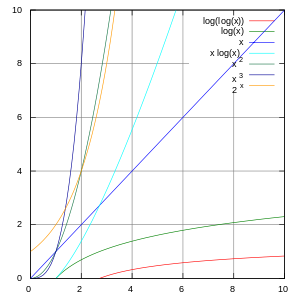
În tabel sunt prezentate grafice de funcții.