Tensiune în bara prismatică
Greutatea intrinsecă în calculele de compresie la tracțiune este luată în considerare pentru structurile a căror greutate este comparabilă cu valorile încărcărilor externe. Acestea pot fi coloane din beton armat, piloni de cărămidă etc.
Să luăm în considerare forțele interne și stresurile care apar într-o tijă extinsă, cu acțiunea simultană a forței concentrate $ F $ și a greutății proprii. Greutatea barei este definită ca
$ Q = \ gamma \ cdot V = \ gamma \ cdot A \ cdot l $,
unde $ \ gamma $ este greutatea specifică a materialului [kN / m 3], $ V $, $ A $, $ l $ este volumul, suprafața secțiunii transversale și, respectiv, lungimea tijei. Greutatea specifică este legată de densitatea materialului, unde densitatea este de aproximativ 10 $ / s.
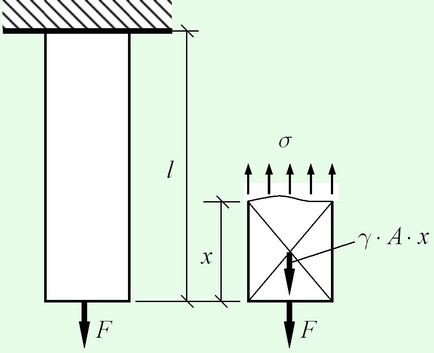
Forța longitudinală, care apare în secțiunea I - I
$ N = F + \ gamma \ cdot A \ cdot x $
Tulburati cand numarati propria greutate
$ \ sigma = \ frac = \ frac + \ gamma \ cdot x $
Cea mai mare stres apare în partea superioară și condiția de rezistență ia forma
$> = \ frac + \ gamma \ cdot l \ leqslant \ left [\ sigma \ right] $
Selectarea zonei secțiunii ținând cont de greutatea proprie
Bar de rezistență egală
O bară de rezistență egală este numită o bară, în care eforturile de-a lungul lungimii nu se schimbă și, de regulă, sunt egale cu tensiunea admisă.
Este de înțeles că, pentru a satisface astfel de condiții, suprafața secțiunii transversale a fasciculului trebuie să varieze în funcție de variația forței longitudinale. Luați în considerare un element infinitezimal al unei tije (Fig.) Cu lungimea $ dx $. Secțiunea inferioară a acestui element are o suprafață de $ A $. Forța longitudinală în ea este $ [\ cdot A $. Forța longitudinală în secțiunea superioară crește cu greutatea elementului, adică cu $ dN = \ gamma \ cdot dV = \ gamma \ cdot A \ cdot dx $. În consecință, zona crește cu $ dA = \ frac >> $.
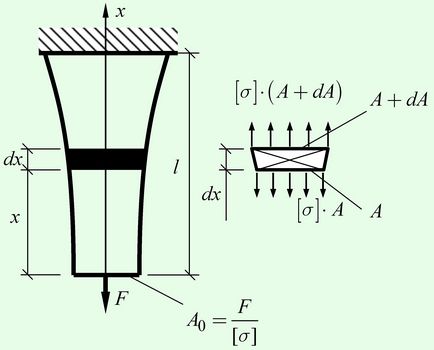
$ dN = \ gamma \ cdot A \ cdot dx = dA \ cdot [\ sigma] $,
În secțiunea inferioară, unde forța longitudinală $ N = F $, suprafața secțiunii transversale ar trebui să fie
apoi, pentru a asigura aceleași eforturi de-a lungul lungimii tijei, zona secțiunii transversale ar trebui să varieze exponențial
Rază de trecere
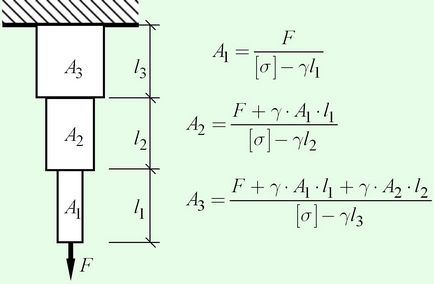
O bară de rezistență egală este incomodă pentru fabricație, astfel încât o schimbare treptată a secțiunii transversale de-a lungul lungimii este utilizată pentru a egaliza solicitările. În acest caz, numărul și lungimea treptelor sunt determinate în funcție de situație, iar aria necesară a secțiunii transversale a fiecărei etape este atribuită din condiția de rezistență atât pentru bara prismatică. De exemplu, pentru o bară în trei trepte, cu o sarcină la sfârșit, se efectuează calculul suprafețelor secțiunii transversale, așa cum se arată în figura 6.3.
Deformarea din greutatea proprie
Tensiune atunci când se ia în considerare numai greutatea proprie pentru fasciculul prismatic
Dacă forța $ F $ acționează asupra tijei, în plus față de greutatea proprie $ Q $, alungirea va fi determinată de formula
Deformările unei bare de rezistență egală sunt determinate mai simplu, deoarece stresul în toate secțiunile este același $ \ sigma = \ left [\ sigma \ right] = const $, după care legea lui Hooke
$ \ Delta l = \ varepsilon \ cdot l = \ frac> \ cdot l $