Transformarea matricei operatorului
Declarația problemei. Găsiți matricea unui operator în bază, unde
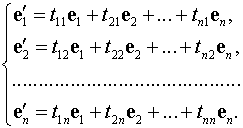
dacă în bază matricea are forma

Când trece de la o bază la o bază, matricea operatorului este transformată de formula
,
unde este matricea de tranziție de la bază la bază.
1. Scriem matricea de tranziție:

2. Găsiți matricea inversă.
3. Găsim matricea operatorului în baza formulei
.
Problema 7. Găsiți matricea în bază, unde
,
dacă este dat în baza.
.
Matricea în bază este dată de formula
.
.
Să găsim matricea inversă.
.
;
;
.
.
Găsim matricea pe o bază nouă:
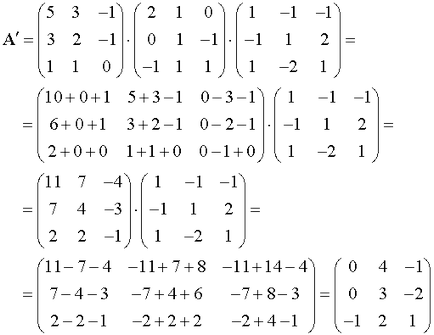
Ie Matricea din baza are forma:
.