deformare transversală. Dați expresiile matematice corespunzătoare,
deschideți semnificația fizică a cantităților pe care le conțin. Specificați unitățile de măsură.
2. Dați definiția: a) stresul mecanic normal, b) tensiunea tangențială (tangențială). Dați expresiile matematice corespunzătoare, extindeți semnificația fizică a cantităților incluse în ele. Specificați unitățile de măsură.
3. Dați definiția: a) legea compresiunii elastice-expansiune, b) legea deformării elastice de forfecare. Dați expresiile matematice corespunzătoare, extindeți semnificația fizică a cantităților incluse în ele.
4. Dați definiția modulului de elasticitate E al materialului. Extindeți semnificația sa fizică, specificați unitățile de măsură.
5. Listați principalele tipuri de deformări. Pentru ce pot fi reduse cele mai simple dintre ele.
6. Care este diferența dintre deformarea elastică și cea plastică?
7. Care este caracteristica deformării cu elasticitate ridicată? Ce organisme are?
8. Dați definiția momentului forței. aducerea expresiilor matematice corespunzătoare, extinderea semnificației fizice a cantităților incluse în ele, specificarea unităților de măsură.
9. Notați condiția de bază pentru echilibrul unui corp având o axă de rotație.
10. Definiti raportul Poisson. Dă-i pe cei potriviți
expresia matematică, deschideți semnificația fizică a cantităților incluse în ea.
Specificați unitățile de măsură.
11. Definirea rezistenței materialului. Notați starea de bază a rezistenței.
12. Care este motivul diferenței dintre punctele forte tehnice și teoretice? Care dintre ele
ei mai mult și de ce?
13. Listați principalele tipuri de distrugere a materialelor. Cum diferă acestea?
14. Să formuleze din punct de vedere energetic starea de germinare a microfracturilor.
Explicațiile se fac cu ajutorul programului corespunzător.
15. Ce caracteristici mecanice de bază ale materialelor pot fi determinate de la
16. Oferiți o definiție a conceptului de duritate a materialului. Listați principalele metode ale lui
determina expresiile matematice corespunzătoare, extindeți
semnificația fizică a cantităților implicate în acestea. Specificați unitățile de măsură.
17. Cum sunt principalele caracteristici mecanice ale modulului legate de materiale:
Modul Young, modul de forfecare și raportul lui Poisson. Dă-i pe cei potriviți
expresia matematică, deschideți semnificația fizică a cantităților incluse în ea.
18. Care este durabilitatea materialului, la ce se măsoară? Cum depinde
durabilitatea materialului din solicitarea mecanică aplicată? aduce
expresia matematică corespunzătoare, deschideți sensul fizic al
19. Cum depinde durabilitatea materialului de temperatura? Dă-i pe cei potriviți
expresia matematică, deschideți semnificația fizică a cantităților incluse în ea.
20. Care este semnificația fizică a termenului "temperatura de fragilitate Txp"
21. Un eșantion de "orthosilium-M", un material pentru căptușeli de bază din silicon cu o lungime inițială de 10 mm, este întins la o deformare relativă de 1,5. Determinați lungimea rezultată a eșantionului.
22. Un eșantion de "orthosilium-M", un material pentru garniturile de bază din silicon cu o lungime inițială de 20 mm, este întins la o lungime de 30 mm. Determinați tulpina relativă a probei.
23. Proba „ORTOS - M“ - material de bază pentru tampoane din silicon supuse unei tulpini de întindere relativă de 1,5, în care lungimea probei rezultată este de 50 mm. Determinați lungimea inițială a eșantionului.
26. Care este modulul Young al dintelui dentinei, dacă la o tensiune de 250 MPa, mărimea relativă a deformării a fost de 1,5%
27. Pentru fabricarea elementelor de sârmă în stomatologia ortopedică
oțel inoxidabil. O bucată de fir de lungime l = 100 mm
are rigiditate k = 5 MN / m. determină rigiditatea unei sârme de 1,5 ori
o secțiune transversală mai mare de 75 mm în lungime.
28. Pentru fabricarea elementelor de sârmă în stomatologia ortopedică
oțel inoxidabil. O bucată de fir cu lungime l = 90 mm
are rigiditate k = 3 MN / m. Determinați rigiditatea unei bucăți de sârmă de 1,5 ori mai mică decât o secțiune transversală de 75 mm în lungime.
29. Pentru fabricarea elementelor de sârmă în stomatologie ortopedică se utilizează sârmă din oțel inoxidabil. O bucată de fir de lungime l = 100 mm are o rigiditate k = 6 MN / m. determinarea rigidității unei lungimi de lungime de 50 mm a firului are aceeași secțiune transversală.
30. Pentru fabricarea elementelor de sârmă în stomatologia ortopedică folosiți un fir fabricat din oțel inoxidabil. O bucată de fir de lungime l = 100 mm are o rigiditate k = 8 MN / m. Determinați rigiditatea unei lungimi de lungime a firului
200mm este aceeași secțiune transversală.
31. Pentru fabricarea elementelor de sârmă în stomatologie ortopedică, folosiți un fir fabricat din oțel inoxidabil. O bucată de fir de lungime l = 100 mm are o rigiditate k = 9 MN / m. determină rigiditatea unei bucăți de sârmă de 1,5 ori mai mare decât o secțiune transversală și de 1,5 ori mai mare decât lungimea.
32. Care va fi rigiditatea celor două bucăți de sârmă conectate paralel din aliajul folosit pentru a forma cleme de proteze? Ambele bucăți de sârmă au aceeași lungime, dar cu o secțiune transversală diferită. Secțiunea transversală a primului segment este de două ori mai mare decât a doua. Rigiditatea primului dintre segmentele K1 = 4 MN / m.
33. Care va fi rigiditatea a două bucăți succesive conectate de sârmă fabricate din aliajul folosit pentru a forma cleme de proteze? Ambele bucăți de sârmă au aceeași secțiune transversală, dar au lungimi diferite. Lungimea primului segment este de două ori mai mare. decât al doilea. Rigiditatea primului segment K1 = 5 MN / m.
34. O probă cilindrică cu o lungime inițială de 10 mm, realizată dintr-un aliaj de aur de testul 900, a fost supusă unor teste de tracțiune. În același timp, lungimea sa a crescut la 10,8 mm, iar diametrul a scăzut de la 7 mm la 6,8 mm. Determinați raportul Poisson al aliajului.
35. Sub sarcină, eșantionul în direcția longitudinală a fost alungit cu un factor 2, iar în direcția transversală el a fost deformat cu un factor de 1,5. Determinați raportul Poisson pentru acest material.
36. De câte ori specimenul sa extins în direcția longitudinală, dacă a fost deformat de 1,3 ori în direcția transversală. Raportul Poisson este de 0,25.
37. De câte ori eșantionul a fost deformat în direcția transversală, dacă este longitudinal
sa prelungit de 1,8 ori? Raportul Poisson este de 0,25.
38. Sub influența unei tensiuni mecanice egale cu 120 MPa, o probă de elastomer
alungită de trei ori. Care este modulul de forfecare pentru acest material?
39. De câte ori eșantionul elastomerului se prelungește atunci când este expus mecanic
180 MPa dacă modulul de forfecare pentru acest material este de 30 MPa.
40. Determinați modulul de forfecare a oțelului dacă modulul Young este 200 GPa pentru acesta și
Raportul Poisson este de 0,3.
41. Determinați modulul de elasticitate al oțelului E dacă modulul de forfecare pentru acesta este G = 80 GPa și
raportul Poisson este de 0,25.
42.Na figura reprezentată schematic cu două punte sprijină pe dinți natural bilateral și B. Concentrat forță F egală cu 900 N se aplică la punctul C. Se determină forța de reacție a bont și dacă a = 4 cm, b = 2 cm
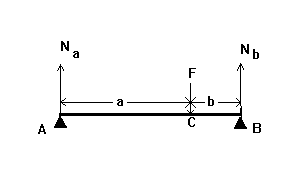
43.Na figura reprezentată schematic cu două punte sprijină pe dinți natural bilateral și B. Concentrat forță F egală cu 720 N se aplică la punctul C. Se determină forța de reacție în culeea când a = 4 cm, b = 2 cm

44. Figura prezintă schematic pod cu două picioare bilaterale dinți naturale A și B. Concentrat forță F egală cu 780 N se aplică la punctul C. Se determină Q forța transversală în secțiune transversală cu coordonate x = 3 cm, măsurată de la punctul A, dacă un = 4 cm și b = 2 cm

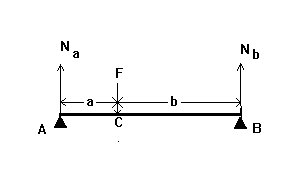
45. Figura prezintă schematic o proteză de pod cu două suporturi bilaterale
pe dinții naturali A și B. Forța concentrată F egală cu 960 N se aplică la punctul C.
Determinați forța transversală Q în secțiunea cu coordonatele x = 5 cm, măsurate din punct
A dacă a = 4 cm și b = 2 cm

46. Figura prezintă schematic pod cu două picioare bilaterale dinți naturale A și B. Concentrat forță F egală cu 700 N se aplică la punctul C. Se determină momentul încovoietor M (x), în secțiunea cu coordonatele x = 6 cm, măsurată de la punctul A în cazul în care a = 4 cm și b = 3 cm.

47. Figura prezintă schematic pod cu două picioare bilaterale dinți naturale A și B. Concentrat forță F egală cu 840 N se aplică la punctul C. Se determină momentul încovoietor M (x), în secțiunea cu coordonate x = 3 cm, măsurată de la punctul A în cazul în care a = 4 cm și b = 3 cm.

48. Figura prezintă schematic pod cu două picioare bilaterale dinți naturale A și B. Concentrat forță F egală cu 700 N se aplică la punctul C. Se determină distanța dintre dintele de referință A, în care momentul încovoietor are valoarea maximă dacă a = 4 cm și b = 3 cm.

49. Figura prezintă schematic pod cu două picioare bilaterale dinți naturale A și B. Concentrat forță F, care este egală cu 450 N, se aplică la punctul C. Se determină distanța dintre dintele de referință A, în care momentul de încovoiere este setat la M = 2,1 Dacă a = 1 cm și
50. Figura prezintă graficele energiei potențiale W [J]
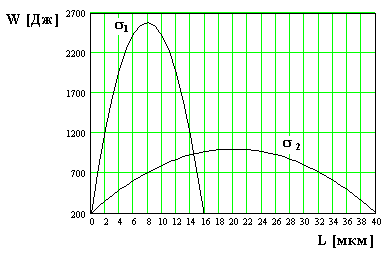
eșantion de material fosforoceramic utilizat pentru a face artificială
dinți, de la lungimea fisurii la două tensiuni: 0,2 MPa și 0,6 MPa.
Determinați lungimea minimă a fisurii de la care va crește.
Proba se află sub acțiunea unei tensiuni de 0,6 MPa.
51. Figura prezintă graficele energiei potențiale W [J]
o probă dintr-un material fosforoceramic utilizat pentru fabricarea dinților artificiali, de la lungimea fisurii la două tensiuni: 0,2 MPa și 0,6 MPa.

Determinați lungimea minimă a fisurii de la care va crește.
Proba se află sub acțiunea unei tensiuni de 0,2 MPa.
52. Figura prezintă graficele energiei potențiale W [J]
o probă dintr-un material fosforoceramic utilizat pentru fabricarea dinților artificiali, de la lungimea fisurii la două tensiuni: 0,2 MPa și 0,6 MPa.

Determinați lungimea maximă a fisurii. din care nu va crește.
Proba se află sub acțiunea unei tensiuni de 0,2 MPa.
53. Figura prezintă dependența logaritmului durabilității materialului de tensiune
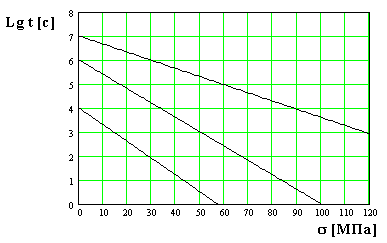
la diferite temperaturi: 350 K, 300 K, 250 K
Determinați durabilitatea materialului la o temperatură de 250 K și un efort mecanic de 90 MPa.
54. Figura prezintă dependența logaritmului durabilității materialului de tensiune
la diferite temperaturi: 350 K, 300 K, 250 K

Determinați durabilitatea materialului la 350 K și efortul mecanic de 30 MPa
55. Figura prezintă dependența logaritmului durabilității materialului de tensiune
la diferite temperaturi: 350 K, 300 K, 250 K

Determinați rezistența materialului la o temperatură de 300 K și o tensiune de 50 MPa.
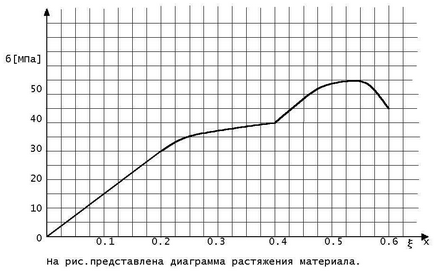
De câte ori modulul de elasticitate al materialului este mai mare decât rezistența la tracțiune.

De câte ori s-a întins eșantionul în timpul pauzei.
