O minge poate fi înscrisă în orice con. O minge conică (sau o sferă înscrisă într-un con) atinge baza conului în centrul său și suprafața laterală - de-a lungul circumferinței. Centrul sferei (sfera) se află pe axa conului.
La rezolvarea problemelor pe o minge înscrisă într-un con, este mai convenabil să se ia în considerare secțiunea transversală a unei combinații de corpuri printr-un plan care trece prin axa conului și centrul mingii.
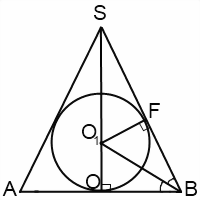
Pentru acest model de formare SA = SB = l, înălțimea conului SO = H, raza sferei OO1 inscripționată = O1F = R. Deoarece centrul cercului inscris - punctul de intersecție al Bisectoarele triunghiului, apoi ∠OBO1 = ∠FBO1, OB = r - raza conului.
Luați în considerare un triunghi dreptunghiular SOB. Prin proprietatea bisectorului triunghiului:
Prin teorema lui Pitagora
Luați în considerare un triunghi dreptunghiular OO1B.
Dacă ∠OBS = α, atunci ∠OBO1 = α / 2. De aici
Dacă exprimăm pentru prima oară raza conului prin înălțimea sa de la triunghiul dreptunghiular SOB
apoi din triunghiul OO1B exprimăm raza mingii prin înălțimea conului: