Scopul lucrării: determinarea experimentală a momentelor de inerție a volantului prin mai multe metode.
Momentul de inerție a volantului poate fi determinat în două moduri.
H
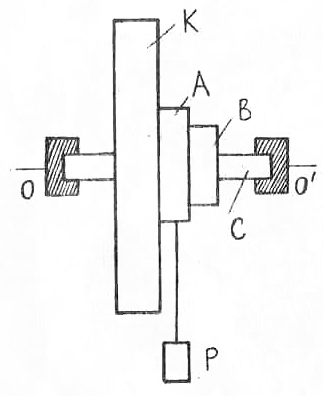
Pe baza legii conservării energiei, putem scrie:
EP - energia potențială a încărcăturii în poziția superioară, E și Ek - energia cinetică a sarcinii și energia cinetică a sistemului rotativ, respectiv în momentul în care firul este răsturnat complet; Atr este energia folosită pentru a lucra împotriva forțelor de fricțiune.
folosim următoarea notație: m - greutatea încărcăturii; h este înălțimea maximă a ascensiunii; - viteza sarcinii în poziția inferioară; r este raza roții; J0 este momentul inerției sistemului; - viteza sa unghiulară în momentul în care sarcina atinge poziția sa inferioară. Apoi ecuația (1) poate fi rescrisă ca:
Deoarece cuplul de frecare nu depinde de viteza de rotație, mișcarea sistemului va fi accelerată uniform. Cunoscând înălțimea h și timpul deplasării sarcinii t, este ușor să calculați viteza în poziția inferioară:
Dacă firul se desface fără alunecare, atunci viteza liniară a punctelor de pe suprafața scripetei este egală cu viteza sarcinii și
Lucrarea impotriva fortelor de frictiune este proportionala cu numarul de revolutii facute de sistem, adica,
unde

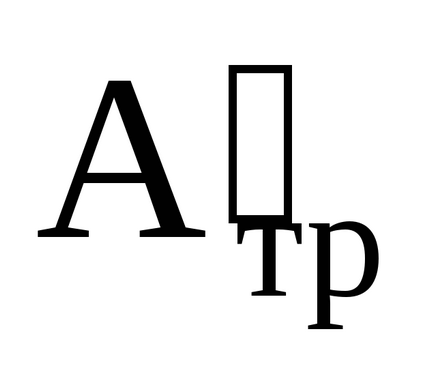
Când sarcina atinge poziția inferioară, firul este separat de scripete, iar sistemul continuă să se rotească, efectuând lucrări împotriva forțelor de frecare datorate energiei cinetice dobândite
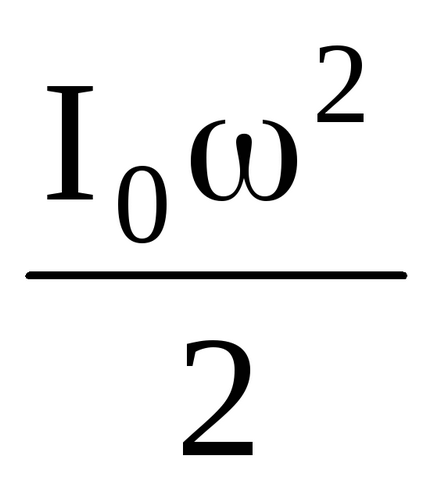
n2 - numărul de rotații ale sistemului la o oprire completă.
Folosind relațiile (3), (4), (5), (6) și (7), putem reprezenta (2)
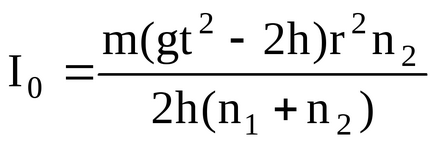
Toate cantitățile care apar în partea dreaptă a acestei ecuații pot fi măsurate experimental.
E
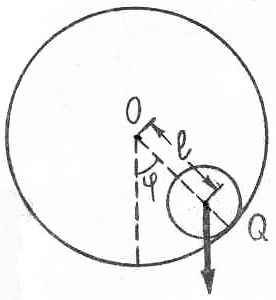
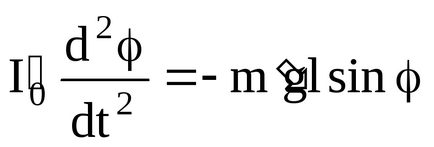
unde J0 'este momentul inerției pendulului, m' este masa sarcinii suplimentare.
Pentru unghiuri mici sin () , adică,
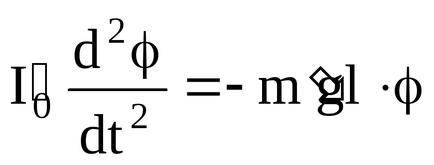
Ecuația (8) este ecuația de oscilație armonică cu perioada
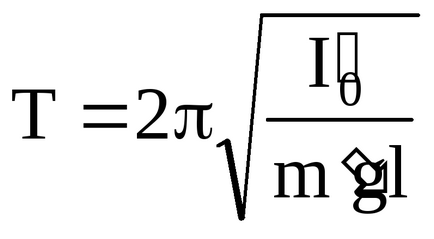
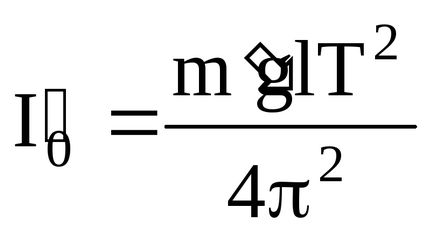
Dispozitive: riglă centimetru (
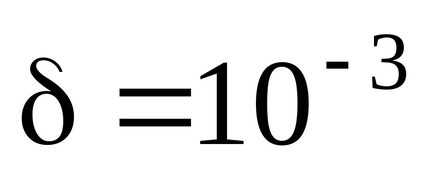
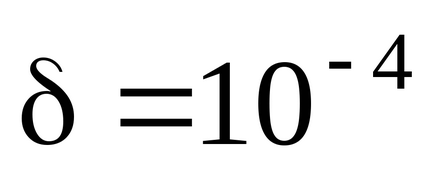
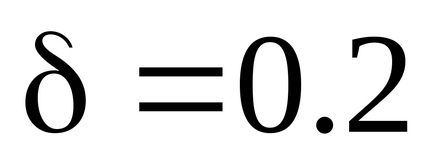
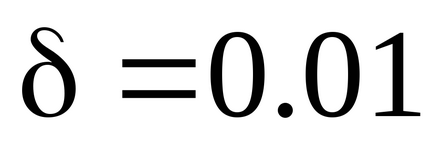
În toate erorile de mai jos, am folosit probabilitatea de încredere
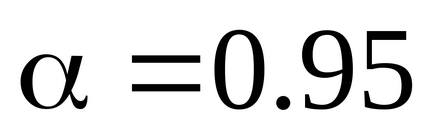
r '(raza axei) = 8,2 mm
l '(lungimea axei) = 209,5 mm
l (grosimea curelei) = 33 mm
h (grosimea volantului) = 10 mm
d (diametrul volantului) = 134,8 mm
R (raza primei role) = 37,5 cm
r (raza celei de-a doua scripeți) = 22,5 cm
M (masa primei încărcări) = 51,3 g
m (masa celei de-a doua încărcături) = 166,9 g
Tabelul 1 (de la căderea mărfurilor, determină viteza de rotație a volantului după separarea firului, precum și numărul de rotații sistemului comise după deplasările de timp menționate mai sus de bunuri ori de la o înălțime de 1 metru).
Următoarele valori sunt determinate experimental: t, m, r, h, n2.
Prin calcularea valorii statistice t medie pentru toate cele 4 cazuri (m și r m și r m și r m și r ...), găsim cele 4 valori ale momentului de inerție al întregului sistem și de eroare folosind cunoscuta formula:
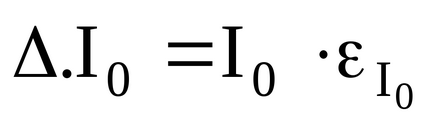
Mai mult, este necesar să se medieze valorile obținute ale momentelor de inerție ale sistemului, ținând cont de erorile lor. Găsiți media ponderată:
J0 = 0,0799 kg m 2
J0 = 0,0067 kg m 2 (care este de 8% din J0).
Vom găsi aceeași valoare teoretic.
Se știe că întregul sistem constă din următoarele elemente: un volant - 2 bucăți, o axă - o bucată, o scripeță mare - o bucată, o roată mică - o bucată.
Momentul inerției discului ( (r) = const), relativ la axa geometrică, se calculează ca:
Atunci momentul inerției întregului sistem va avea forma:
unde Ji este momentul inerției unuia dintre elementele descrise mai sus. Având parametrii geometrici și masele acestor corpuri, găsim momentul inerției sistemului:
Js = 0,0858 kg m 2.
Momentul de inerție a scripeților și a axei (fără volant) este de 0,0055 kg ∙ m 2. care nu depășește eroarea obținută în determinarea momentului de inerție al întregului sistem. În consecință, putem presupune că momentul inerției unui volant unic este de 1/2 din momentul inerției sistemului.
Momentul inerțial al volantului (experimental) se calculează astfel:
JK = 0,0400 kg m 2.
În timpul experimentului, măsuram timpul de 3 oscilații pentru mai multe supraîncărcări.
Tabelul 2 (timp 3 x oscilații ale pendulului fizic (volant modificat))
Astfel, se calculează 4 valori ale momentului de inerție al sistemului și apoi se măsoară prin metoda menționată în metoda precedentă. Avem:
JS = 0,0879 kg m 2
JS = 0,0030 kg m 2
În acest caz, momentul inerțiunii scripeților și axei (0,0055 kg m 2) depășește eroarea experimentală și, prin urmare, nu poate fi omis.
Să scriem momentul inerției volantei:
unde J * este momentul de inerție a axei și a scripeților și J ** este momentul de inerție al sarcinii suplimentare (calculat pe baza caracteristicilor sale de masă și liniară).
J ** = 0,0014 kg m 2
JK = 0,0398 kg m 2.
Rezultatele obŃinute prin aceste metode sunt medii (luând în considerare erorile acestora) - găsim valoarea medie ponderată:
JK = 0,0399 kg m 2.
JK = 0,0020 kg m 2.
În timpul acestei lucrări, momentul inerției volantului a fost determinat experimental utilizând două metode diferite. Rezultatele au fost medii, deoarece au fost obținute prin metode diferite pentru un sistem.
În cazul metodei de oscilație, a fost luată în considerare momentul inerției părților componente ale sistemului care au fost luate în considerare (în primul caz, datorită erorii în mod clar depășire, a fost omisă).