10. Capacitatea electrică. condensatoare
Capacitatea electrică a unui conductor solitar este o cantitate fizică egală cu raportul dintre sarcina conductorului și potențialul său în domeniul acestei încărcări:
Capacitatea electrică a conductorului indică ce încărcare este necesară pentru a informa conductorul pentru ca acesta să poată lua valoarea specificată. Cu cât este mai mare sarcina conductorului, cu atât este mai mare potențialul acestuia în câmpul acestei încărcări. Prin urmare, capacitatea electrică nu depinde de mărimea conductorului de încărcare sau de valoarea sa potențială, ci depinde numai de mărimea și forma conductorului, iar proprietățile dielectrice ale mediului în care se află. Unitatea de măsură a capacității electrice a unui conductor în SI este numită farad (notat cu 1 F):
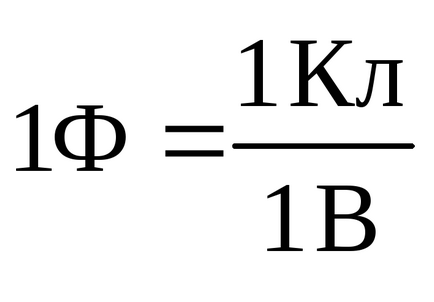
Să luăm în considerare determinarea capacității unui bilă conductoare de rază R. în vid. Pentru a face acest lucru, să dăm mingii o sarcină arbitrară Q. Încărcarea va fi uniform distribuită pe suprafața sferei cu densitatea de suprafață
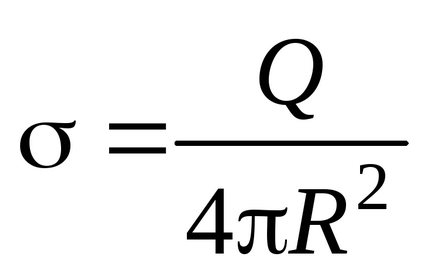
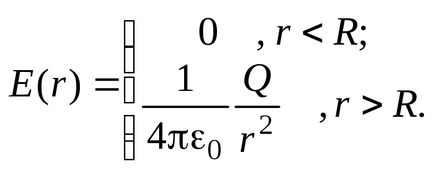
Tipul funcției
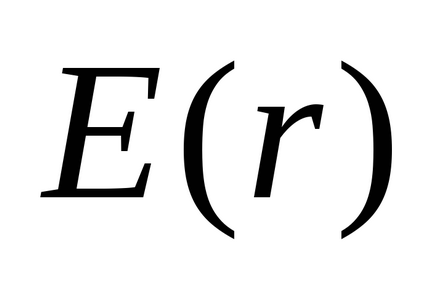
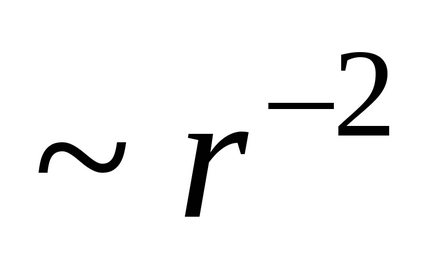
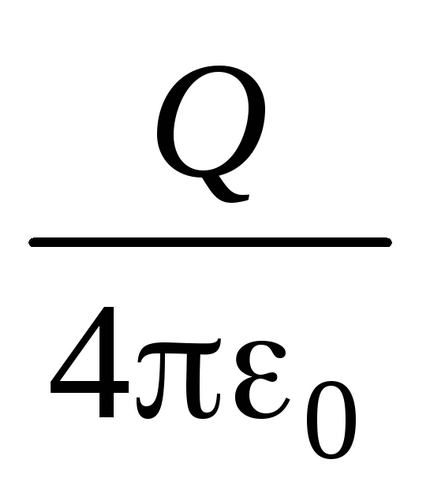
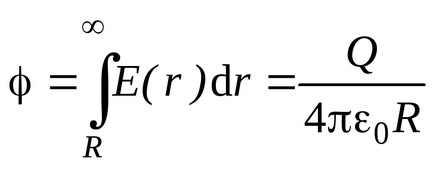
În conformitate cu (3.5), capacitatea mingii
Capacitatea electrică a unui condensator este o cantitate fizică egală cu raportul dintre sarcina condensatorului și diferența de potențial creată de câmpul acestei sarcini între plăcile sale:
La fel ca și capacitatea conductorului, capacitatea electrică a condensatorului nu depinde de valoarea taxei condensator, nici diferența de potențial dintre plăcile sale, și depinde numai de mărimea și forma condensator, și proprietățile dielectrice ale mediului între plăcile condensatorului. Trebuie remarcat faptul că capacitatea unui condensator nu depinde de prezența altor organisme conductive sau dielectrice în apropierea acestuia.
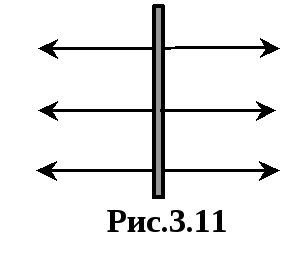
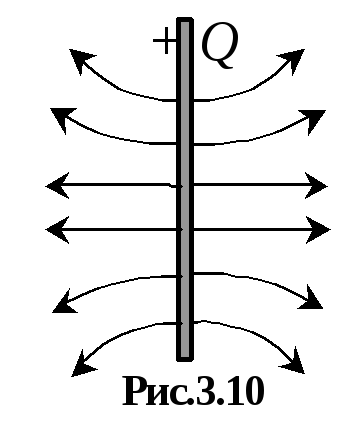
Ca un exemplu, obținem un condensator plat formulă capacitate prezentată în Fig. 3.9, de asemenea. Definim câmpul electrostatic produs de o zonă de placă încărcată S. Liniile de forță a unui astfel de câmp sunt reprezentate în Fig. 3.10. Dacă luăm în considerare un punct în spațiu situat atât de aproape de placa încât distanța de la ele la placa este substanțial mai mică decât înainte de limitele sale (aceste puncte de placă va fi reprezentat ca un avion mare infinit), curbura liniilor de câmp la limitele plăcii pot fi neglijate (Fig. 3.11 ). Astfel, un plan infinit de mare încărcat creează un câmp omogen. Pornind de simetria sistemului, intensitatea câmpului modulului la toate punctele echidistante de placa trebuie să fie aceeași, și vectorul de direcție

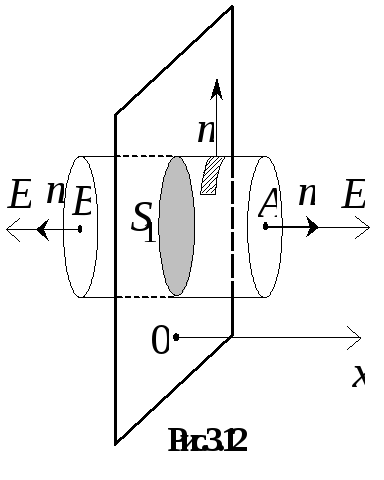
Să determinăm intensitatea câmpului la un anumit punct cu coordonate x. măsurată de-a lungul axei
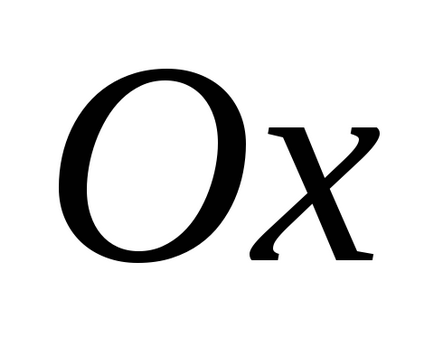
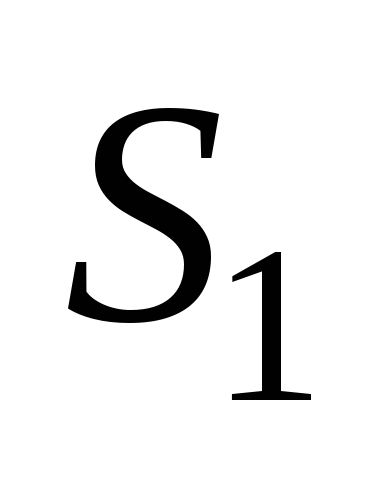

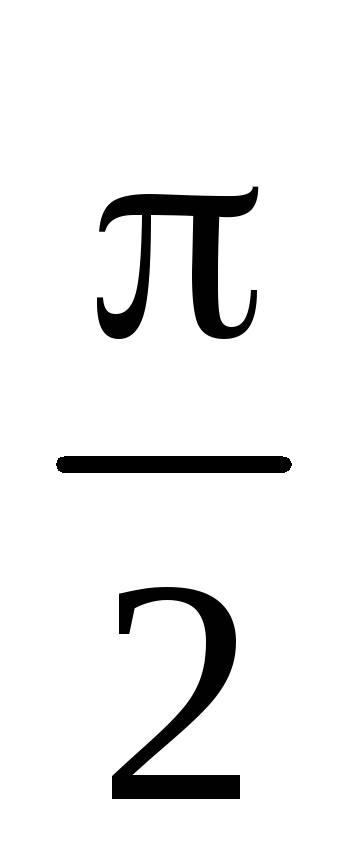
Să determinăm fluxul de intensitate a câmpului prin suprafața selectată.
,
unde
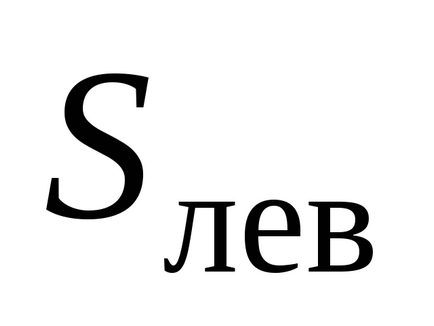
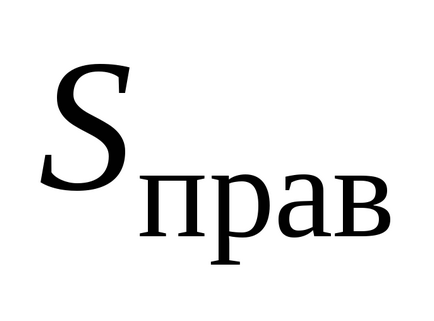
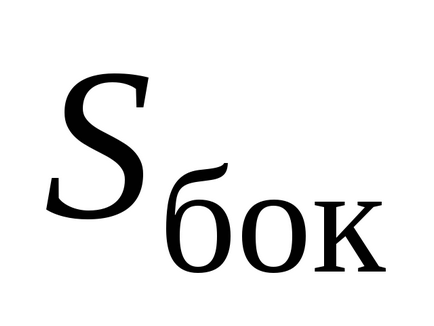
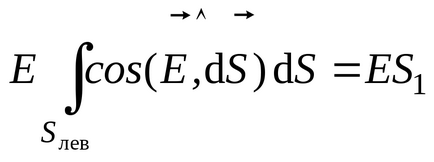
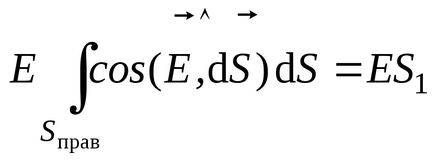
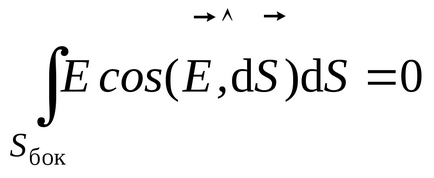
Să determinăm suma algebrică a sarcinilor închise de suprafața unui cilindru Gaussian. În acest caz, sarcina electrică care intră în ea este încărcarea părții "tăiate" a plăcii de către cilindru. Se poate găsi prin înmulțirea zonei bazei cilindrului cu densitatea de suprafață a încărcăturii plăcii:
Ecuați (3.8) și (3.9) cu o cotă pentru coeficient
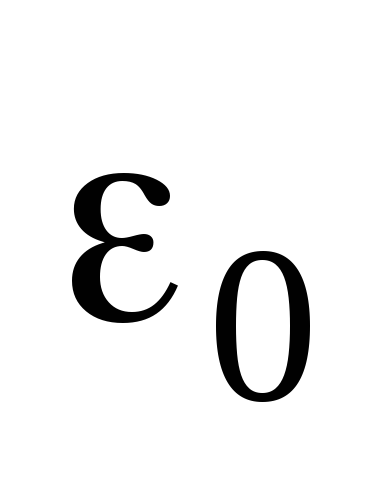
Relația rezultantă determină modulul forței unui câmp omogen al unei plăci încărcate infinit de mari.
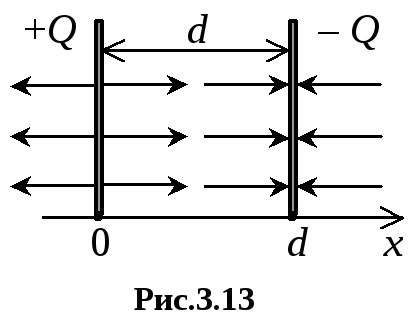
Când două plăci încărcate opus dispuse la o distanță mică unul de altul, astfel încât să satisfacă condiția omogenitatea câmpului fiecărui (Figura 3.13.), Intensitatea câmpului electromagnetic poate fi determinat prin luarea în considerare principiul superpoziției (3.10)
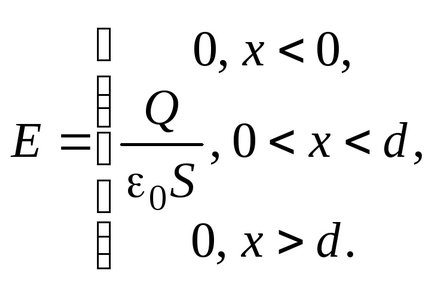
În acest caz, diferența de potențial dintre plăcile condensatorului rezultat poate fi definită după cum urmează:
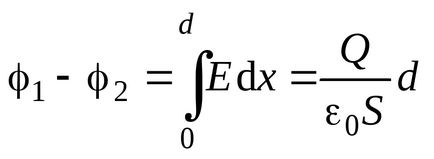
Capacitatea unui condensator plat, prin definiție (3.7), se ridică la
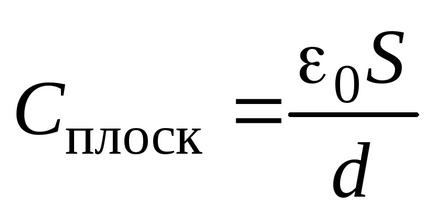
Rețineți că, în cazul în care spațiul dintre plăcile fiecărui condensator umple dielectric cu o permitivitate relativă , apoi pentru aceeași valoare a intensității câmpului electrozilor de încărcare între electrozii scad în ori. Prin urmare, diferența potențială dintre ele scade cu un factor de a, și, prin urmare, capacitatea condensatorului crește cu un factor de :
.
Luăm formula pentru capacitatea unui condensator sferic. Luați în considerare sistemul de plăci sferice prezentat în Fig. 3.9, c. Am pus încărcătura Q pe placa interioară și pe încărcătura externă
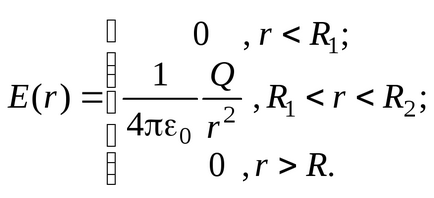
Să determinăm diferența potențială dintre plăci, folosind conexiunea diferențială dintre rezistență și potențial (1.13):
.
Capacitatea unui condensator sferic, prin definiție (3.7), se ridică la
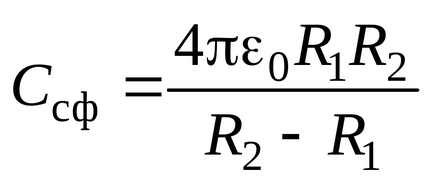
Dacă condensatorul este umplut cu un dielectric cu o permitivitate relativă , atunci
Subliniem încă o dată faptul că capacitatea condensatorului depinde de dimensiunea, forma condensatorului și permitivitatea relativă a dielectricului între plăcile sale.
11. Energia câmpului electric.
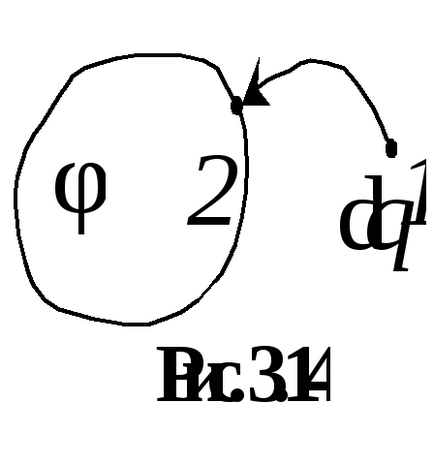
Luați în considerare procesul de încărcare a unui conductor solitar. Că sarcina sa a atins valoarea lui Q. vom raporta taxa de conductor în dq. transferându-le din punctul de infinit 1 spre suprafața conductorului până la punctul 2 (Figura 3.14). Pentru a transfera conductorului o nouă porțiune de încărcare
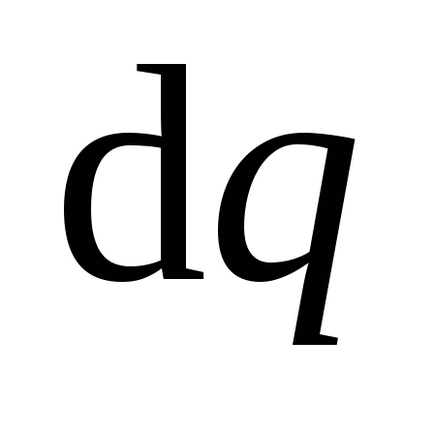
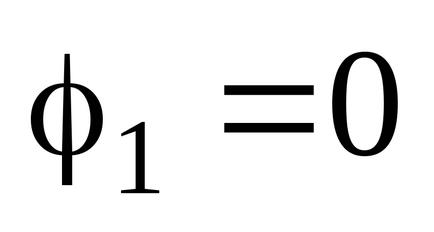
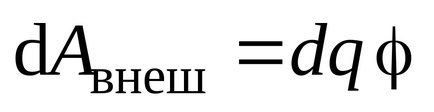
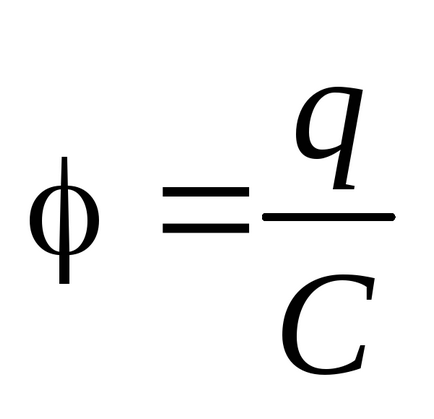
.
Conform legii conservării energiei, forța forțelor externe de încărcare a conductorului mărește energia câmpului electrostatic creat, adică dirijorul stochează o anumită energie:
Luați în considerare procesul de încărcare a condensatorului de la sursa EMF. Sursa în procesul de încărcare transferă taxele de la o placă la alta, iar forțele externe ale sursei efectuează lucrări pentru a crește energia condensatorului:
,
unde Q este încărcarea condensatorului după încărcare. Apoi, energia câmpului electric creată de condensator este determinată ca
Expresia (3.14) ne permite să notăm energia câmpului electrostatic în două moduri:
Comparația celor două relații ne permite să punem întrebarea: care este purtătorul de energie electrică? Taxele (prima formulă) sau câmpul (a doua formulă)? Ambele ecuații înregistrate sunt în acord excelent cu rezultatele experimentale, adică calculul energiei câmpului poate fi realizat în mod egal corect de ambele formule. Totuși, acest lucru este observat numai în electrostatice, adică când se calculează energia câmpului încărcărilor staționare. Luând în considerare teoria câmpului electromagnetic în cele ce urmează (Capitolul 8), vedem că un câmp electric poate fi creat nu numai prin sarcini staționare. Câmpul electrostatic este un caz special al unui câmp electromagnetic care există în spațiu sub forma unui val electromagnetic. Energia sa este distribuită într-un spațiu cu o anumită densitate. Introducem conceptul densității volumetrice a energiei câmpului în modul următor.
Transformăm ultima egalitate (3.14) pentru cazul unui condensator plan, folosind conexiunea dintre diferența de potențial și puterea câmpului omogen:
,
unde
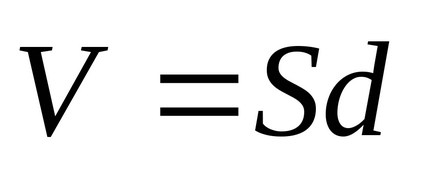
Densitatea volumului energiei câmpului este raportul dintre energia câmpului închis într-un volum mic de spațiu și acest volum:
În consecință, energia unui câmp electric omogen poate fi calculată după cum urmează:
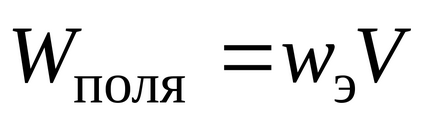
Concluzia trasă poate fi extinsă la cazul unui câmp neomogen în felul următor:
unde
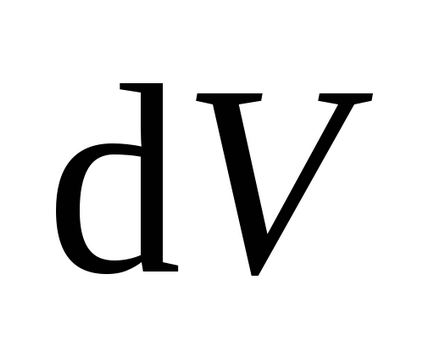
De exemplu, calculam energia unui câmp electric creat de o sferă solitară metalică cu raza R. Încărcarea încărcată Q. și localizată într-un mediu cu o permitivitate relativă . Repetând argumentul exemplului din § 2.5, obținem modulul forței de câmp sub forma unei funcții
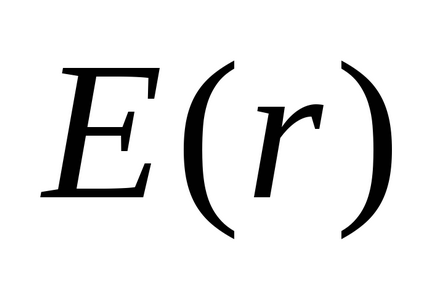
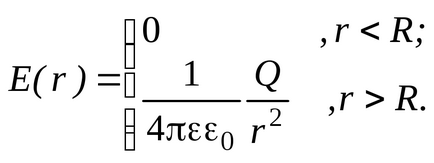
Apoi expresia pentru densitatea energetică în vrac a câmpului are forma:
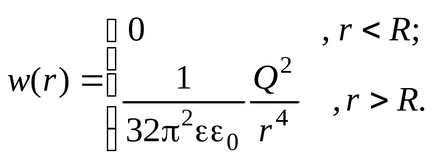
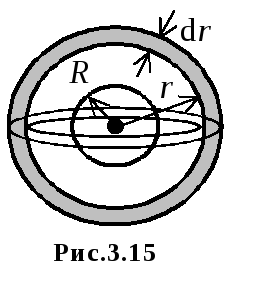
Deoarece intensitatea câmpului depinde doar de coordonatele radiale, va fi practic constantă într-un strat sferic subțire cu o rază internă r și o grosime
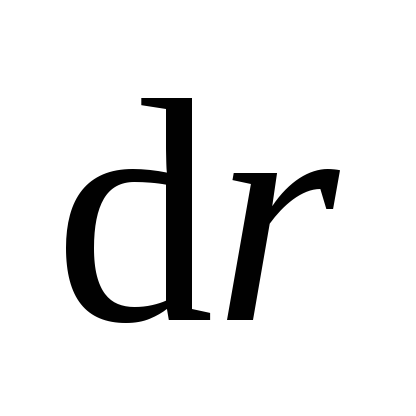
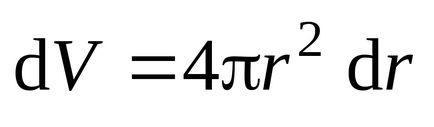
.
Un rezultat analog ar fi obținut dacă energia unei sfere încărcate a fost calculată din formula (3.13), utilizând (3.6):
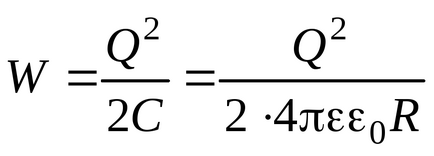
Cu toate acestea, trebuie amintit că o astfel de metodă este inaplicabilă dacă este necesar să se găsească energia câmpului electric, închis nu în întregul volum al câmpului, ci numai în partea sa. De asemenea, metoda de calcul utilizând formula (3.13) nu poate fi utilizată pentru a determina energia câmpului unui sistem pentru care conceptul de "capacitate" nu este aplicabil.