Linia dreaptă. având doar un punct comun cu un cerc, se numește o tangentă a cercului. și punctul lor comun se numește punctul de tangență al unei linii și al unui cerc.
Teorema (proprietatea tangentei la cerc)
Tangenta la cerc este perpendiculară pe raza trasată până la punctul de tangență.
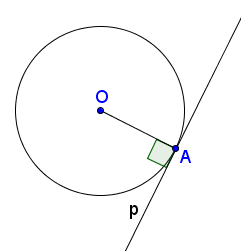
Este dat. p este tangentă la cerc
A este punctul de contact
Noi dovedim metoda "prin contradicție".
Să presupunem că p OA, atunci OA este înclinată la linia dreaptă p.
Dacă OH este perpendiculară trasată de la punctul O la linia dreaptă p, atunci lungimea lui va fi mai mică decât raza: OH<ОА=r
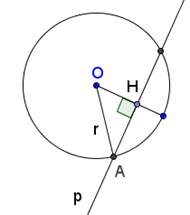
Observăm că distanța de la centrul cercului la linia dreaptă p (OH) este mai mică decât raza (r). atunci linia p este secant (adică are două puncte comune cu un cerc), care contrazice ipoteza teoremei (p este tangenta).
Prin urmare, ipoteza este falsă, prin urmare linia p este perpendiculară la OA.
Teorema (Proprietatea segmentelor de tangente trase dintr-un punct)
Segmentele tangentelor la cercul tras dintr-un punct sunt egale și egale cu unghiurile de la linia care trece prin acest punct și centrul cercului.
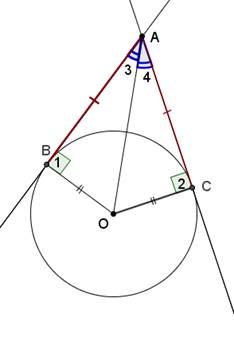
AB și AC sunt tangente la împrejurimi. (O; r)
1) OB AV, OS AS, ca raze. efectuată la punctul de tangență (proprietatea tangentă)
2) Considerăm mp. AOB și tr. AOC - p / u
OB = OS (ca raze)
Mijloace. ABO = AOS (pe hypotenuse și picior). Prin urmare,
AB = AC. <3 = <4 (как соответственные элементы в равных тр-ках). ч.т.д.
Teorema (simptom al unei tangente)
Dacă linia trece prin capătul razei, situată pe cerc și perpendiculară pe această rază, atunci este o tangentă.
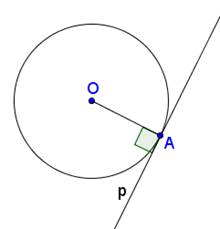
Este dat. OA este raza cercului
Dovedeste-o. p este tangentă la cerc
OA este raza cercului (prin ipoteză) (OA = r)
OA este perpendiculara de la O la linia dreaptă p (OA = d)
Prin urmare, r = OA = d. atunci linia p și cercul au un punct comun.
Prin urmare. linia p este tangentă la cerc. QED
3. Proprietatea acordurilor și secantelor.
Proprietățile tangentei și secantului
Un cerc este locusul de puncte echidistant de la un singur punct, numit centrul unui cerc.
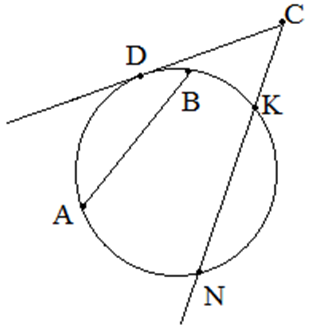
Un segment care unește două puncte dintr-un cerc este numit coardă (în figură acesta este un segment). Coarda care trece prin centrul cercului se numește diametrul cercului.
1. Tangenta este perpendiculară pe raza trasată până la punctul de tangență.
2. Segmentele tangentelor trase dintr-un punct sunt egale.
3. Dacă o tangentă și o secantă sunt extrase dintr-un punct în afara cercului, atunci pătratul lungimii tangentei este egal cu produsul secantului pe partea sa exterioară: