29.1 Determinați semnul pantei tangentei desenate pe graficul funcției y = f (x), reprezentat în figura dată. la punctele cu abscisa a, b, c:
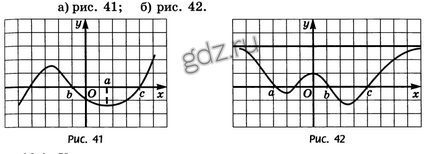
29.2 Specificați punctele în care derivatul este zero și punctele la care derivatul nu există dacă graficul funcției este reprezentat în figura dată:
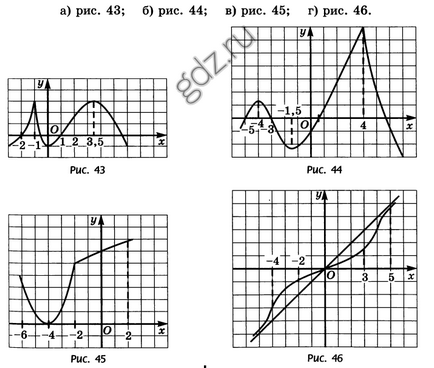
29.3 forme contondente sau un unghi ascuțit sau ascuțit cu axa x pozitivă direcția tangentei la graficul funcției y = f (x), efectuat la un punct cu abscisa x = a, în cazul în care:
29.4 Care este panta tangentei la parabola y = 1-x2 la punctul:
29.5 Găsiți coeficientul de pantă al tangentei trasate la graficul funcției y = f (x) în punctul cu abscisa x = a dacă:
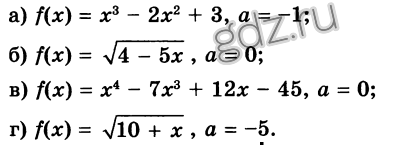
29.7 Determinați ce unghi formează cu axa x tangenta trasă la graficul funcției y = f (x) în punctul cu abscisa x = a dacă:
29.10 Determinați ce unghi formează cu axa x tangenta trasă la graficul funcției y = f (x) în punctul cu abscisa x = a dacă:
29.12 Scrieți ecuația tangentei în graficul funcției y = f (x) într-un punct cu abscisa x = a dacă:
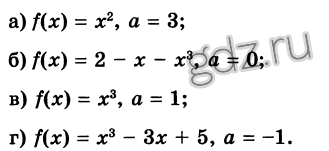
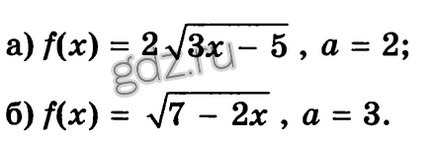
29.17 Scrieți ecuațiile tangentelor în graficul funcției y = 9-x2 în punctele de intersecție cu abscisa.
29.18 Scrieți ecuațiile tangentelor la parabola y = x2 - 3x la punctele cu ordonata 4.
29.19 În graficul funcției y = x3-3x2 + x + 1 găsiți punctele în care tangenta formează un unghi de 45 ° cu direcția pozitivă a axei de abscisă. Scrieți o ecuație pentru fiecare dintre aceste tangente.
29.20 În ce punct este tangenta graficului funcției y = x2 paralel cu linia dată:
În ce puncte tangenta la graficul funcției date y = f (x) este paralelă cu linia dată y = kx + m:

29.23 Scrieți ecuațiile acestor tangente la graficul funcției. care sunt paralele cu linia dată:
29.24 Folosind formula, se calculează aproximativ:
29.25 Prin punctul B, trageți o tangență la graficul funcției y = f (x) dacă:
29.26 Faceți ecuația tangentei în graficul funcției. x