Societatea fizico-matematică a elevilor vârstnici

Optica geometrică. Sarcini cu o soluție.

1) Două oglinzi plane formează un unghi dihedral α = 60 °. Una dintre oglinzi este lovită de un fascicul situat într-un plan perpendicular pe linia de intersecție a oglinzilor. Găsiți unghiul de deformare a acestei raze din direcția originală după reflexia din ambele oglinzi (vezi Fig.).

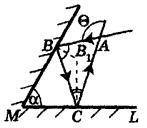
MN și ML sunt oglinzi plate; Incidenta razei AB pe oglinda MN; BC - incident pe grinda ML oglindă; AC este o rază reflectată de două oglinzi; # 629; - unghiul dorit de deformare a fasciculului după două reflexii ale oglinzilor.

Într-un quadrangle, prin urmare

Din legea reflexiei rezultă că, prin urmare, unghiul dorit de deviere # 629; este extern la # 8710; BAC. prin urmare

răspundă: # 629; = 120 °

2) Pe perete, a cărui plan este înclinat vertical de 4,87 °, o oglindă plată este întărită (vezi Fig.). La ce distanta maxima o persoana are o crestere h = 170 cm
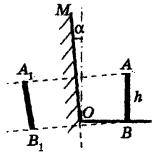
pentru a vedea în oglindă cel puțin o parte a imaginii tale?

soluţie:

Fie AB persoana care stă la oglindă, apoi A 1 B 1 - imaginea ei în oglinda MO (vezi figura). A 1 B 1 și AB sunt simetrice în raport cu oglinda MO. Este clar că în acest caz o persoană își vede imaginea. Cazul de limitare se obține atunci când linia dreaptă AA 1 trece prin punctul O (vezi Fig.). prin urmare, distanța necesară

Rețineți că unghiul α este mic, prin urmare tgα = α, cu condiția ca α să fie exprimat în radiani:

3) Determinați deplasarea fasciculului după trecerea printr-o placă de sticlă paralelă plană cu grosime d = 6 cm, având un indice de refracție n = 1,6. Unghiul de incidență al fasciculului pe placă este α = 60 ° (vezi Fig.).

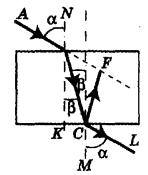
AB -padayuschy fasciculul placă, BN - perpendicular la punctul de incidență, α - unghiul de incidență la soare - raza refractată, β este unghiul de refracție, CM - perpendicular pe punctul de incidență pe fața inferioară a plăcii. De atunci, raza cade pe fața inferioară a plăcii la un unghi β. Pe baza reversibilității razei de lumină, se poate afirma că aceasta lasă placa la un unghi α. Totuși, fasciculul se deplasează la distanță, scriem legea refracției într-un punct (unghiuri verticale), deci Din De la decalajul fasciculului

4) Obiectul se află la o distanță l = 15 cm de placa de sticlă plană paralelă. Observatorul vede obiectul prin farfurie, iar linia de vedere este normală. Determinați distanța x de la imaginea obiectului la fața cea mai apropiată de observator, dacă grosimea plăcii este d = 4,5 cm, indicele de refracție al sticlei este n = 1,5.

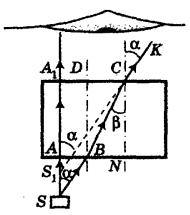
Construi imaginea obiectului (vezi Fig ..): S - subiect, SA - incidentul fascicul perpendicular pe placa, SB - incidentul fascicul la un unghi α la placa. Rețineți că razele SA și SB trebuie să cadă în ochi, astfel încât unghiul α este mic; BD este normal față de placă;

După trecerea plăcii, grinzile SA și SK se deosebesc. Extensiile lor se intersectează la punctul S 1. care este o imagine imaginară a punctului S. Distanța necesară A 1 S 1 = x.

De aici
(de atunci)

Imaginea este obținută presupunând că unghiul α este mic, deci, unghiul de refracție β este mic. Prin urmare, prin urmare,
Răspuns: 18 cm.

5) La fundul vasului umplut cu apă la o înălțime de h. există o sursă de lumină punctuală. Un disc circular plutește pe suprafața apei, astfel încât centrul discului să fie deasupra sursei de lumină. La ce rază minimă a discului nu se produce o singură rază prin suprafața apei? Indicele de refracție al apei este n.

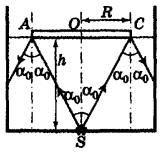
Razele emise de sursa S și care intră pe disc sunt reflectate din ea și nu ieșesc prin suprafața apei (vezi Fig.). Dacă unghiul de incidență al razei SA este egal cu unghiul de limitare a reflexiei totale, atunci această rază nu iese de asemenea prin suprafața apei. Razele care intră pe suprafața apei din stânga punctului A au un unghi de cădere mai mare decât α0 și, de asemenea, nu ieșesc prin suprafața apei. Astfel, pentru raza SA, trebuie îndeplinită următoarea condiție: sin α0 = 1 / n.

Pe de altă parte,

Ecuând expresiile pentru tangente, obținem

6) Un fascicul de raze paralele cade pe o jumătate de sferă de rază r = 2 cm, din sticlă cu un indice de refracție. Determinați raza spotului luminos pe ecran amplasat la o distanță L = 4. 82 cm de centrul mingii.

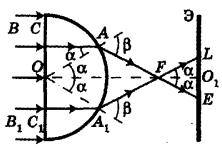
Luați în considerare fasciculul BC, care cade pe o suprafață plană. Acesta penetrează mingea și, fără devieri, lovește suprafața sferică din punctul A. OA este raza mingii; - unghiul de incidență al fasciculului pe o suprafață sferică și. În consecință, pe măsură ce fasciculul incident este îndepărtat din axa simetriei OO 1, unghiul de incidență α crește. La un moment dat devine egal cu unghiul de limitare a reflexiei totale: în acest caz, unghiul de refracție β este egal cu 90 °. numai acele raze ale fasciculului va ieși mingea care cade pe suprafața plană între punctele C 1 și C De asemenea, ele formează după refracție pe o suprafață sferică a unui spot luminos pe ecran, raza care este egală cu O 1 E = O 1 L. Când a = 45 ° AOA 1 F este un pătrat și

1.450.852 de vizitatori unici

Pagina anterioară

Pagina următoare

Societatea fizico-matematică a elevilor vârstnici - optica geometrică