Arabă Bulgară Chineză Croată Cehă Daneză Olandeză Engleză Estoniană Finlandeză Franceză Germană Greacă Hindi Indonezian Islandeză Italiană Japoneză Letonă Lituaniană malgașă Norvegiană Persană Poloneză Portugheză Română Rusă Sârbă Slovacă Slovenă Spaniolă Thai Turcă Vietnameză suedeză
Arabă Bulgară Chineză Croată Cehă Daneză Olandeză Engleză Estoniană Finlandeză Franceză Germană Greacă Hindi Indonezian Islandeză Italiană Japoneză Letonă Lituaniană malgașă Norvegiană Persană Poloneză Portugheză Română Rusă Sârbă Slovacă Slovenă Spaniolă Thai Turcă Vietnameză suedeză
definiție - întreaga parte
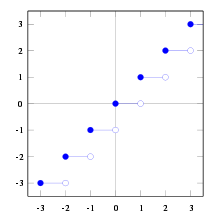
Graficul grafic al funcției "sex" (partea parțială a numărului)
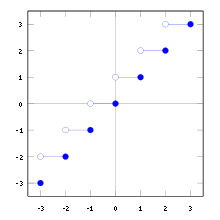
Graficul funcției "plafon"
În matematică. partea întregă a numărului real este rotunjirea până la cel mai apropiat întreg. Întreaga parte a numărului se numește și anthier (entier) sau sex (podea engleză). Împreună cu podeaua există o funcție asociată - plafonul (tavanul englez) - rotunjind cel mai apropiat întreg către o parte mai mare.
Notație și exemple
Pentru întreaga parte a numărului, denumirea introdusă de Gauss a fost folosită pentru o lungă perioadă de timp [sursa nu este specificată 1032 zile]. Nici conceptul unei funcții de plafon, nici o desemnare specială pentru aceasta nu există. În 1962, Kenneth Iverson a propus să rotunțească numărul către cel mai apropiat întreg pe laturile mai mici și mai mari pentru a numi "podea" și "plafon" și a denota și în consecință [1].
În matematica modernă se folosesc ambele denumiri și, totuși, există o tendință de trecere la terminologia și notația lui Iverson. Unul dintre motive este potențialul ambiguității conceptului "partea intregă a numărului" [1]. De exemplu, partea întregă a numărului 2.7 este de 2, dar sunt posibile două opinii privind modul de determinare a întregii părți a numărului -2.7. Conform definiției date în acest articol, totuși, în unele calculatoare există o funcție a întregii părți INT, pentru numere negative definite ca INT (-x) = -INT (x), deci INT (-2,7) = -2. În terminologia lui Iverson, nu există nicio ambiguitate posibilă:
defini
Funcția de sex este definită ca cel mai mare număr întreg. mai mică sau egală cu:
Funcția tavan este definită ca cel mai mic întreg, mai mare sau egal:
Aceste definiții sunt echivalente cu următoarele inegalități (unde n este un număr întreg) [2]:
Peste tot în jos indică numere reale. a sunt numere întregi.
Etaj / tavan în funcție de o variabilă reală
Funcțiile de podea / tavan unesc un set de numere reale la un set de numere întregi:
Funcțiile de podea / tavan sunt discontinue la toate punctele întregi, acestea fiind discontinuități de primul tip cu un salt. egal cu unitatea.
În acest caz, funcția câmpului este:
Funcția tavan este:
Conectarea funcțiilor de podea și tavan
Pentru tot podea și tavan sunt aceleași:
Dacă - nu întregul, atunci plafonul este exact o unitate deasupra podelei:
Funcțiile de podea și tavan sunt reflectări ale celor două axe:
Etaj / tavan: inegalitate
Orice inegalitate între un real și un întreg este echivalentă cu o inegalitate cu un sex și un plafon între numere întregi [2]:
Cele două inegalități superioare sunt consecințe imediate ale definițiilor sexului și plafonului, iar cele două cele inferioare sunt cele inverse ale celor superioare.
Funcțiile de podea / tavan sunt funcții în creștere monotonică:
Etaj / plafon: adăugare
Termenul întreg poate fi adăugat / scos din paranteze de podea / tavan [4]:
În general, egalitatea precedentă nu este valabilă dacă ambii termeni sunt numere reale. Cu toate acestea, în acest caz, inegalitățile dețin și:
Etajul / tavanul sub semnul funcției
Se afirmă următoarea propunere: [5]
Să fie o funcție de creștere continuă monotonic definită la un anumit interval. având proprietatea:
ori de câte ori este determinată.
dacă și sunt numere întregi și.
Etaj / Tavan: Suma
Dacă sunt numere întregi, atunci [6]
În general, dacă este un număr real arbitrar, atunci a este un număr întreg pozitiv
Există o relație mai generală [7]:
Deoarece partea dreaptă a acestei ecuații este simetrică în ceea ce privește u, este valabilă următoarea lege privind reciprocitatea:
cerere
Integerul funcțiilor de podea / tavan este utilizat pe scară largă în matematica discretă și teoria numerelor. Mai jos sunt câteva exemple de utilizare a acestor funcții.
Numărul de cifre din intrarea numerică
Numărul de cifre din numărul pozitiv întreg în sistemul de numere poziționale cu baza b este [8]
rotunjire
Cel mai apropiat de un număr întreg poate fi determinat de formula
Modul de funcționare binar
Operația "resto modulo", notată cu, poate fi definită folosind funcția de sex, după cum urmează. Dacă sunt numere reale arbitrare, și, atunci coeficientul incomplet al împărțirii este egal cu
,
Partea fracționată
Partea fracționată a unui număr real este, prin definiție, egală cu
Numărul de puncte întregi ale intervalului
Este necesar să se găsească numărul de puncte întregi într-un interval închis cu puncte finale și, adică, numărul de numere întregi care satisface inegalitatea
Datorită proprietăților podelei / tavanului, această inegalitate este echivalentă cu
.
Acesta este un punct într-un gol închis cu capete și egal cu.
În mod similar, puteți calcula numărul de puncte întregi în alte tipuri de lacune. Un rezumat al rezultatelor este prezentat mai jos [9].
Primele trei rezultate sunt valabile pentru toți, iar a patra este numai pentru.
Teorema lui Rayleigh privind spectrul
Fie u un număr pozitiv irațional. conectat prin relația [10]
Apoi, în rândul numerelor
fiecare natură apare exact o dată. Cu alte cuvinte, secvențe
În Informatică
În limbile de programare
În multe limbi de programare există funcții de podea / tavan încorporate (), ceil ().
În sistemele de aspect
În TeX (și LaTeX) pentru simbolurile de podea / tavan există comenzi speciale: \ lfloor, \ rfloor, \ lceil, \ rceil. Deoarece wiki utilizează LaTeX pentru un set de formule matematice, această comandă este utilizată în acest articol.