Suma x + y a vectorilor x și y este un vector tras de la începutul lui x până la sfârșitul lui y. dacă vectorul y este paralel mutat astfel încât capătul x și începutul y să fie aliniate.
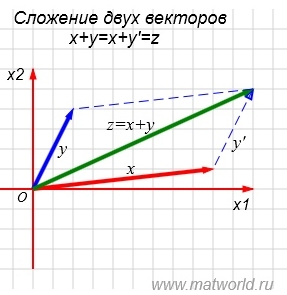
Varianta 1. Punctele de plecare ale tuturor vectorilor coincid cu originea.
Să construim suma z = x + y a vectorilor u.
Pentru a construi suma vectorilor z = x + y. Trebuie să mutăm vectorul y paralel, astfel încât originea vectorului y să coincidă cu sfârșitul vectorului x. Apoi, sfârșitul vectorului y 'rezultat va fi punctul final al sumei vectorilor z = x + y.
Astfel, pentru a obține suma vectorilor x și y, este suficient să se adauge coordonatele corespunzătoare vectorilor x și y:
În figura Fig. 1 în spațiul bidimensional reprezintă procesul de adăugare a vectorilor x = (9,1) și y = (2,4).
Calculăm z = x + y = (9 + 2, 1 + 4) = (11.5). Comparați rezultatul cu interpretarea geometrică. Într-adevăr, după traducerea paralelă a vectorului y în poziția y 'și adăugarea lui x și y'. obținem vectorul z = (11.5).
Opțiunea 2. Punctele de pornire ale vectorilor sunt arbitrare.
Luați în considerare adăugarea a doi vectori x și y. Fie vectorul x un punct inițial și un punct final, iar vectorul y este punctul de plecare și punctul final. Pentru a muta vectorul y în paralel. fiecare element i al punctelor C și D trebuie să fie mărit cu valoarea corespunzătoare γi: