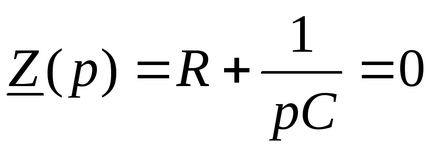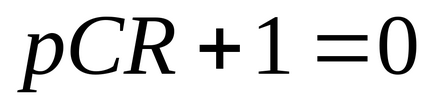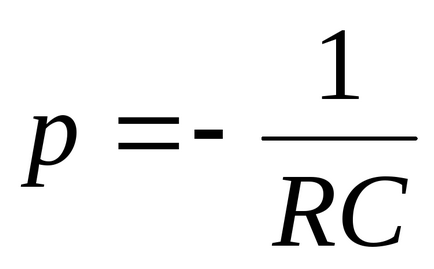Calcularea procesului tranzitoriu se bazează pe două legi de comutare:
1. Curentul prin inductanța imediat înainte de comutare este egal cu curentul prin aceeași inductanță imediat după comutare, sau curentul de pe inductor nu se poate schimba brusc. .
Luați în considerare circuitul electric prezentat în Fig. 43.
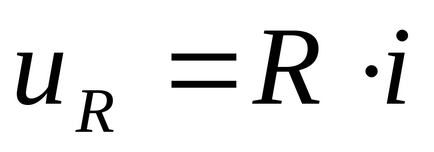
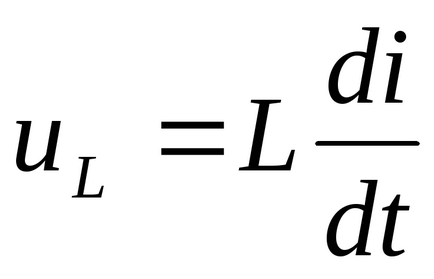
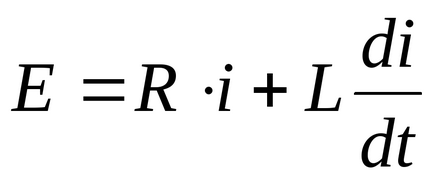
Permiteți modificarea curentă în timpul unui proces tranzitoriu brusc, adică în timp
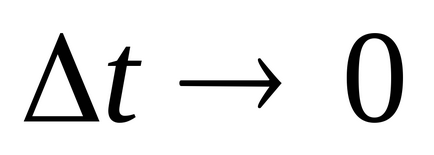

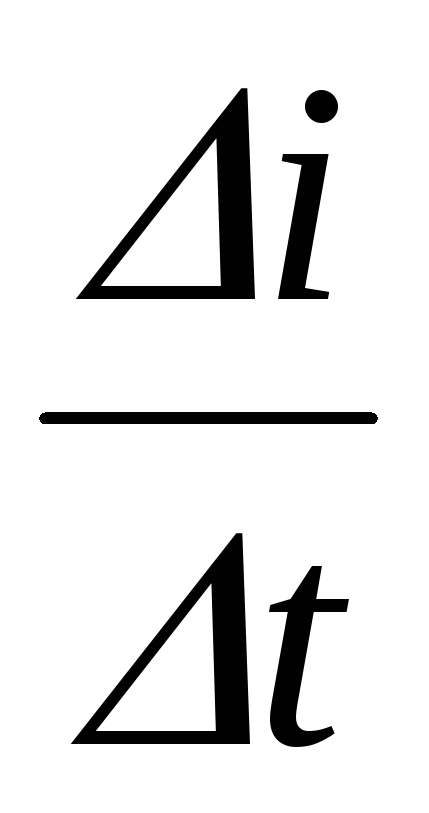
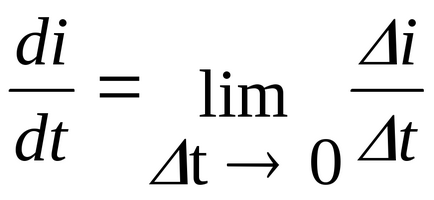
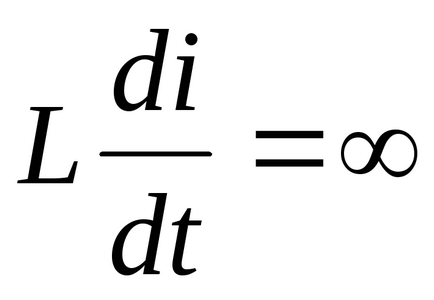
Prin IIzakonu Kirchhoff Ae - valoarea finală, prin urmare, nu este soblyudaetsyaIIzakon Kirchhoff, și presupunerea că curentul care curge prin inductor, poate varia în fals discontinuă. Prima lege de comutare (curentul care trece prin inductanță nu se poate schimba brusc) este dovedit.
2. Tensiunea pe condensator imediat înainte de comutare este egală cu tensiunea pe aceeași capacitate imediat după comutare sau tensiunea pe condensator nu se poate schimba brusc. UC (0-) = UC (0+).
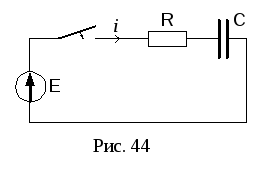
Luați în considerare circuitul electric din Fig. 44.
Despre a doua lege a lui Kirchhoff
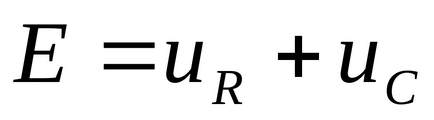
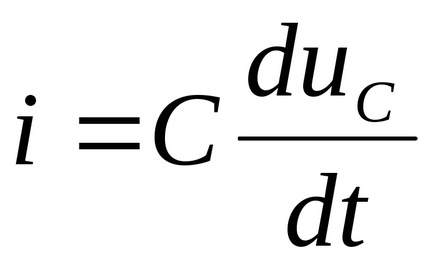
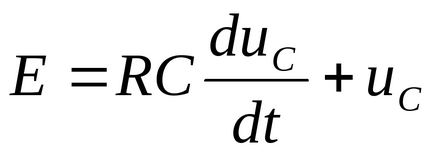
Lăsați ca scăderea tensiunii peste condensator să se modifice brusc în timpul procesului tranzitoriu, adică în timp
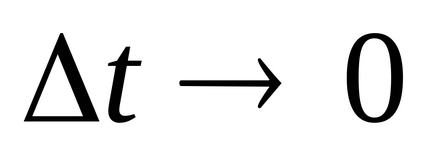
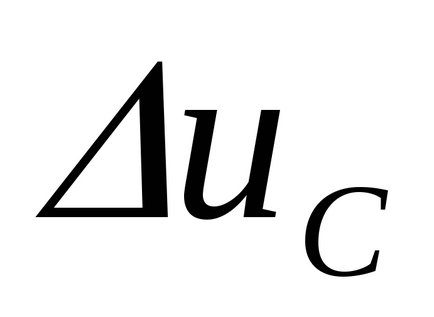
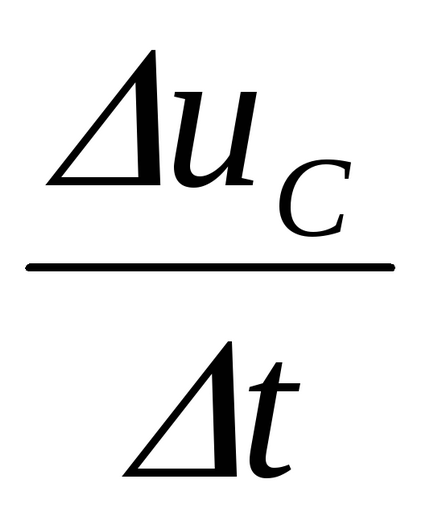
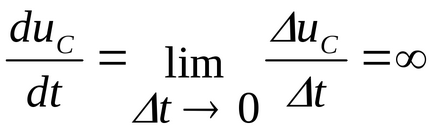
Conform legii lui Kirchhoff. Deoarece E este o cantitate finită, legea lui Kirchhoff nu este respectată. Presupunerea este greșită. A doua lege de comutare este dovedită.
Condiții inițiale independente și dependente
Pentru oricare dintre circuitul electric după comutarea poate scrie ecuațiile legilor lui Kirchhoff a le identifica valorile curenților în toate ramurile și tensiunea pe orice parte a circuitului pentru prima dată după comutarea (t = 0 +). Aceste valori ale curenților și tensiunilor sunt condițiile inițiale.
Condițiile inițiale sunt împărțite în mod independent și dependent. Valorile curentului care curge prin inductanță
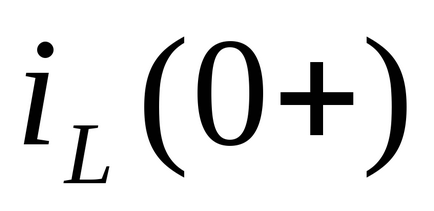
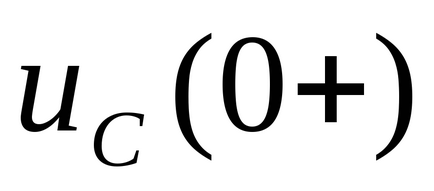
Ecuația caracteristică a circuitului electric
Ecuația caracteristică a circuitului electric este realizată pentru modul post-comutație și este determinată de configurația circuitului.
În cadrul schemei circuitului electric poate determina imediat gradul de ecuația caracteristică - este egal cu numărul de condiții inițiale independente (curenții care curge prin inductor, și tensiunea pe container) în circuitul poslekommutatsionnoy și nu depinde de tipul de surse de circuit CEM.
Vom considera tranzitorii care apar în circuitele de curent continuu care conțin fie o inductanță, fie o capacitate.
Metodele de construire a ecuației caracteristice sunt oarecum, cele mai frecvente dintre acestea fiind bazate pe înregistrarea rezistenței de intrare a circuitului la un curent alternativ:
Rezistența de intrare la curentul alternativ al circuitului electric este înregistrată după comutare
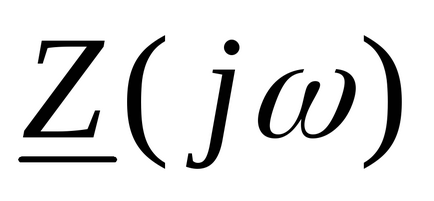
Înlocuit de acesta
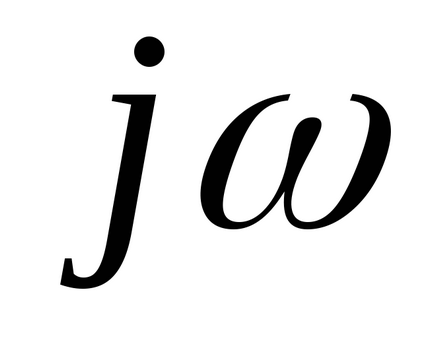
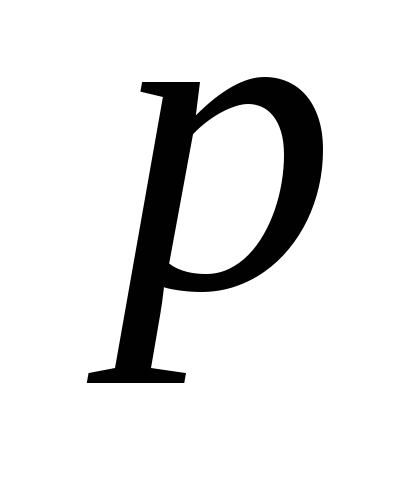
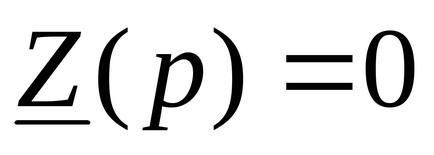
Se găsesc rădăcinile acestei ecuații caracteristice. [p] = c-1.
De exemplu, formulam ecuația caracteristică și găsim rădăcinile ei pentru circuitul electric din Fig. 44.
;