Maximă a funcției este definită ca extremum funcției. dar sunt adăugate condiții suplimentare.
Utilizați un calculator pentru a găsi un maxim al funcției:
Maximă este y = 1 / e, punctul x = 1
Pentru a găsi extreme, este necesar să se rezolve ecuația $$ \ frac f = 0 $$ (derivatul este egal cu zero), iar rădăcinile acestei ecuații sunt extremele funcției: $$ \ frac f = $$ Prima derivata $$ - xe ^ + e ^ = 0 $$ rezolva această ecuație
Rădăcinile acestei ur-TION: conectare $$ X_ = 1 $$. extreme în punctele:
-1 (1, e)
Intervale de creștere și descreștere a funcției:
Am găsit intervale în care creșterile de funcții și scade, și funcțiile minimele și maxime, uita-te pentru această funcție se comportă ca în extremele, la cea mai mică abatere de la extremelor:
Depresiunilor funcția de acolo.
Maximele funcției la punctele: $$ X_ = 1 $$ descompunere la intervale
(-OO, 1]
Creșterile în golurile
[1, oo)
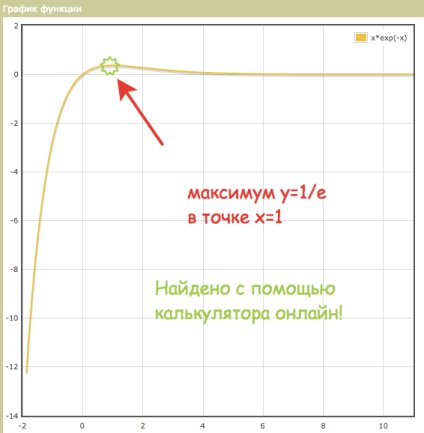
Determinarea funcției maxime
Funcția maximă - este valoarea maximă la un anumit interval de timp. Maximă este după cum urmează:
Se rezolvă ecuația. „Derivata funcției este egal cu 0“ pentru x necunoscute (dacă funcția este dependentă de x) și se uită la rezultatele x ca un punct de schimbare a semnului funcției derivat, care trece prin acest punct
Un alt exemplu simplu al unei funcții maxime
Luați în considerare funcția -x ^ 2. derivatul său este egal cu -2 * x (derivat De altfel este aici) - rezolva ecuația -2 * x = 0 - atunci x = 0.
Uite - derivat -2x când x> 0 - mai puțin de 0, și atunci când x <0 производная больше 0.
Deci, la x = 0 funcția -x ^ 2 are un maxim. Iată un exemplu simplu.