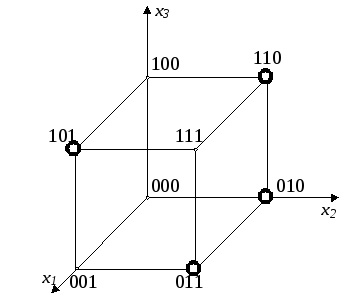
În cazul în care valorile prescrise ale argumentelor se potrivește cu punctul FAL spațiul n-dimensional, atunci setul
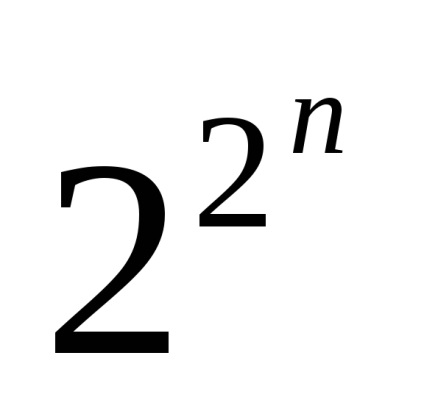
f (101, 110, 010, 011) = 1
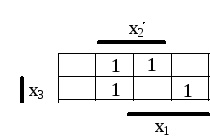
Sau hărți Karnaugh sau hărți Veitch
Valorile FAL pot fi setate deloc posibile seturi de argumente. La o anumită valoare a funcției nu poate fi determinată. Aceste funcții sunt numite nu este complet sigur.
Funcții booleene elementare
Luați în considerare setul de elementar FAL. Vom începe cu cazul în care lungimea cuvântului n = 0. Conform formulei, care determină numărul de funcții logice care calculează ca atunci când n = 0
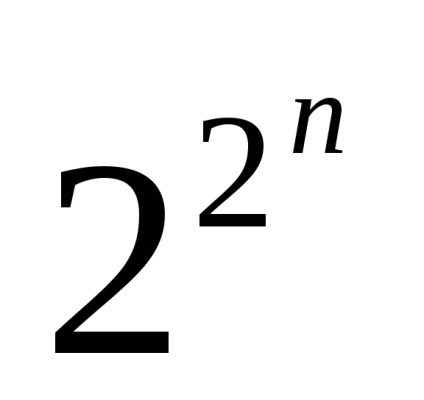
Aceste două funcții sunt aceleași constante.
Pentru n = 1 avem două funcții, depinzând în mod esențial pe argumentul x, aceste două funcții sunt definite în tabelul