Prin link-ul dinamic înțelege orice tip de dispozitiv fizic și design structural, dar având o anumită descriere matematică.
Nivelul caracteristică - acesta este răspunsul său la anumite acțiuni de intrare. Pentru unitățile liniare și sisteme liniare, în general, determină complet caracteristica proprietăților dinamice, ca la sistemele liniare de link-uri, și principiul superpoziției este aplicabil, permițând reacția unui element liniar cu privire la orice expunere cunoscută pentru a găsi răspunsul său la expunerea de orice fel.
Ca o contribuție la nivelul la care a solicitat o reacție la impactul descris de funcții matematice elementare, adică acelea care pot fi descompuse în orice funcție arbitrară. În teorie de control așa cum sunt utilizate funcțiile de bază:
1) o unitate de impuls sau o funcție delta, d (t);
2) Unitatea Funcția etapa 1 (t);
3) sin funcția armonică X0 (în greutate).
Există un timp (puls și o funcție de tranziție) și caracteristicile de frecvență.
Funcția sau pulsatorie link greutatea w (t). Funcția sau pulsatorie de ponderare este o unitate de reacție pentru funcția de unitate de impuls.
Funcția unității de impuls sau d-funcția este o funcție care este zero pretutindeni, cu excepția la origine, dar în așa fel încât integrala sa peste orice interval conținând zero, este egal cu unitatea, adică,
În plus, pentru orice e> 0.
Fig. 3.1. Diagramele de sincronizare de intrare și de ieșire semnale de legătură
Cu alte cuvinte, funcția greutate w (t) reprezintă tranzitorie la nivelul de ieșire (Fig. 3.1) aplicată singur impuls sa de intrare.
Funcția de ponderare w (t) se numește link-ul original (adică inversul transformatei Laplace) a funcției de transfer, și anume:
unde si - toți polii (rădăcini ale numitorul) ale W funcția de transfer (e). În această formulă denotă resturi Res.
Cunoașterea funcției de impuls w (t), pot fi găsite pe orice x intrare operațiune de reacție legătură (t), a cărui expansiune d-funcție are forma:
Semnalul de la ieșirea legăturii liniare este definită ca
unde t - să sprijine timpul de integrare.
Cu funcția greutate w nivel (t), este posibil să se determine funcția de transfer:
Funcția de tranziție de nivel h (t). Funcția de tranziție este o unitate de reacție la funcția de unitate pas satisface
După cum se vede (fig. 3.2), funcția de tranziție este un proces de tranziție către unitatea de ieșire la un singur șoc la intrare.
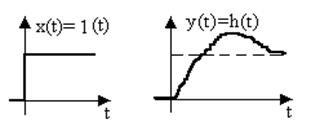
Fig. 3.2. Diagramele de sincronizare de intrare și de ieșire semnale de legătură
Din unitățile discutate mai sus pentru următoarele relații liniare aparente între funcțiile de impuls și de tranziție. ca
unitate funcțională tranzitorie este conectată cu conversia funcției de transfer Carson, adică avem următoarea transformare integrală:
Greutatea și caracteristicile tranzitorii sunt funcții de timp și, prin urmare, fac parte din caracteristicile temporale.
Caracteristicile de frecvență ale managerilor. Caracteristicile de frecvență menționată formule și curbe care caracterizează reacția de a lega de intrare efectele armonice în starea de echilibru, adică, forțat nivelul de oscilație sinusoidală.
Dacă intrarea legăturii liniare de a prezenta efecte armonice
în cazul în care X0 - amplitudine,
w - frecvența unghiulară având o dimensiune [rad / s] sau [c-1],
atunci, deoarece condițiile necesare și suficiente de liniaritate, nivelul de ieșire în starea de echilibru va fi, de asemenea, o funcție armonică aceeași frecvență, dar, în general altă amplitudine, Y0 și transferate în faza în raport cu variabila de intrare pentru unghiul y
Comunicarea între intrare și ieșire setul armonice folosind unitatea de funcția de transfer de frecvență W (jw).
Funcția de transfer de frecvență este o caracteristică esențială a legăturii dinamice și este raportul dintre semnalele de imagine de ieșire și de intrare Fourier sub zero, condițiile inițiale la zero și efecte egale asupra altor factori de producție:
Dintr-o comparație între Fourier și Laplace transformă rezultă că funcția de transfer de frecvență a unității este ușor de a obține funcția de transfer prin substituirea s la jw, adică
Funcția de transfer de frecvență W (jw), așa cum se vede, este un număr complex, care pot fi scrise în sisteme polare și coordonate carteziene:
W (jw) = A (w) = U (w) + ÎM (w), (3.8)
unde A (w) - unitate sau amplitudinea funcției de transfer de frecvență reprezentând valoarea de ieșire a raportului de amplitudine la amplitudinea semnalului de intrare, adică câștig nivelul k la frecvența w
A (w) = | W (JW) | = Mod W (jw) =; (3.9)
y (w) - argumentul sau fază a funcției de transfer de frecvență indică defazajul ieșirii armonice în raport cu frecvența de intrare pe w
y (w) = arg W (jw); (3.10)
U (w) - componenta reală a funcției de transfer de frecvență
V (w) - componenta imaginară a funcției de transfer de frecvență
legam constituie funcția de transfer de frecvență.
Astfel, funcția de transfer de frecvență determinarea răspunsului unitate la vibrații armonice toate frecvențele posibile, permite, folosind principiul superpoziției, găsiți unitatea de reacție la un efect liniar arbitrar.
Expresia (3.8) reprezintă caracteristica amplitudine-frecventa a nivelului de fază. Ecuațiile (3.9) și (3.10) se numesc nivelul de frecvență amplitudine caracteristică și caracteristica de frecvență a link-ul de fază, iar expresiile (3.11) și (3.12) - caracteristica de frecvență a frecvenței nivelului caracteristic reale și imaginare.
Caracteristicile de frecvență afișate grafic pentru reprezentarea vizuală a link-ul a caracteristicilor de frecvență.
răspuns amplitudinea și faza de frecvență (APFC). Construit pe planul complex reprezintă locul geometric al tuturor vectorilor (locus) corespunzătoare funcției de transfer de frecvență W (jw) în timp ce modificarea frecvenței de la zero la infinit (fig.3.3). Pentru fiecare frecvență w este aplicată pe punctul planului complex, atunci punctele obținute sunt conectate printr-o curbă lină. APFC pot fi construite ca în coordonate carteziene (U, V) și polar (A, y).
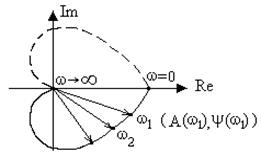
Fig. 3.3. Amplitudine și frecvența de fază de răspuns
APFC este construit pentru ambele frecvențe pozitive și negative. La înlocuirea unei W (jw) w -w obținute la conjugatul valoare complexă. Prin urmare, frecvențele APFC negativ este o imagine în oglindă în raport cu axa reală APFC pentru frecvențe pozitive. În Figura 3.3 frecvențele APFC negativ este arătat de linia punctată. Lungimea vectorului trase de la origine la punctul APFC corespunzător frecvenței selectate w este egal cu A (w), iar unghiul dintre vector și axa reală pozitivă este egal cu y (w).
frecvență caracteristică Amplitudine (AFC). Arată cum se leagă transmite semnalul de frecvență diferită, în caz contrar, aceasta reprezintă rata de schimbare a amplitudinii oscilației armonice atunci când trece prin link-ul (fig. 3.4).
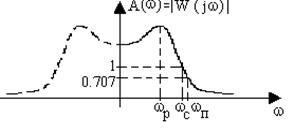
Fig. 3.4. răspuns în frecvență Amplitudine
unde WP - frecvența de rezonanță, adică, frecvența la care frecvența de amplitudine picuri caracteristice, altfel, la această unitate de frecvență are câștig maxim;
WC - frecvența de întrerupere, frecvența la care frecvența de amplitudine scade caracteristice și presupune o valoare egală cu una, și cu creșterea în continuare a frecvenței rămâne mai mică decât unitatea;
Wt - frecvența de transmisie, frecvența la care frecvența de amplitudine scade caracteristice și presupune o valoare egală cu 0,707, și cu creșterea în continuare a frecvenței nu este crescută;
DWP = 2wp - gama de lățime de bandă frecvențe armonice de oscilație transmise legătură fără atenuare apreciabilă.
Caracteristica de frecvență de fază (PFC). Ea arată defazajele introduse prin link-ul de la frecvențe diferite (Fig.3.5).
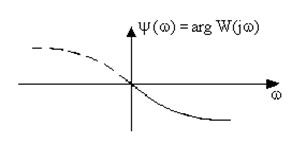
Fig. 3.5. Caracteristicile de frecvență de fază
Caracteristica de frecvență reală (VCHH). Reprezintă dependența de frecvență a componentei reale a funcției de transfer a frecvenței (fig. 3.6).
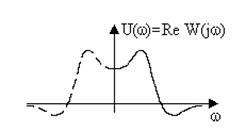
Fig. 3.6. Răspunsul de frecvență reală
Caracteristica de frecvență imaginară (IHM). Reprezintă dependența de frecvență a componentei imaginare a funcției de transfer a frecvenței (figura 3.7).
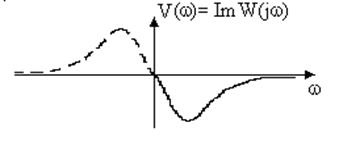
Fig. 3.7. Răspunsul de frecvență imaginar
Caracteristicile de frecvență logaritmice (LCHH). În practică, cele mai multe dintre caracteristicile de amplitudine și frecvență de fază reprezentate pe o scară logaritmică (fig. 3.8).
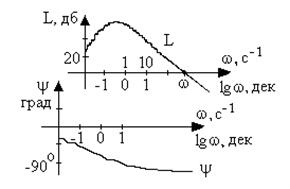
Fig. 3.8. Caracteristicile de frecvență logaritmice
În construcția caracteristicii logaritmice de frecvență amplitudine (LAA), axa ordonata reprezintă valoarea
L (w) = 20 lg A (w) = 20 lg | W (jw) |. (3.13)
Această cantitate este exprimată în [dB] decibeli. Bel este o unitate logaritmică, care corespunde unei creșteri a capacității de zece ori. O putere alb corespunde unei creșteri de 10 ori, 2 albe - de 100 de ori, etc. Decibeli este egală cu o zecime din alb. Deoarece A (w) este raportul dintre o capacitate maximă, și amplitudini, creșterea acestui raport corespunde de două ori zece sau douăzeci de decibeli Belam. Prin urmare, partea dreaptă (3.13) este multiplicatorul 20. Prin abscisă frecvența w pe lg scara logaritmica (w). Unitate uniformă a abscisă este deceniu [decembrie] - orice segment în care valoarea frecvenței crește w de zece ori. punctul LAA de intersecție cu abscisa corespunde cu WC frecvența de tăiere. LAA jumătate plan superior corespunde valorilor k> 1 (amplitudine câștig), și inferior semiplanul - valorile A<1 (ослабление амплитуды).
În construcția fazei logaritmice a caracteristicii de frecvență (LPC) numărare unghiuri y (w) = argW (jw) este axa verticală în scala normală în grade unghiulare.
Principalul avantaj al caracteristicilor de frecvență logaritmice este posibilitatea de a construi ei, în multe cazuri, puțin sau nici o lucrare de calcul.
Toate tipurile de caracteristicile dinamice ale unităților (funcție de transfer, ecuația diferențială, funcția de ponderare, funcție de transfer, răspunsul amplitudine și frecvență de fază) sunt interconectate. Prin urmare, ele sunt echivalente reciproc în determinarea proprietăților dinamice ale nivelului sistemului de control.