Obiectiv: Pentru a studia procesele din circuitul rezonant având capacitate electrică, inductanță și rezistență; determinarea perioadei, frecvența și decrementare logaritmică.
Aparatură și materiale: laborator de suport având un set de obiecte de pe tablă; un generator de semnal; osciloscop; set de cabluri de conectare.
Cauza fluctuațiilor este de multe ori de ieșire (deviere) a sistemului din poziția sa de echilibru și dându-l la sine. Apoi, ea începe să oscileze cu privire la poziția de echilibru. Aceste vibrații sunt numite proprii (gratuit) oscilații ale sistemului.
Din cauza pierderii de energie inevitabilă a mișcării de vibrație (frecare în sistemele mecanice, conductorul de încălzire, un dielectric în condensator, radiația undelor electromagnetice în sistemele electrice oscilatorii, etc), variații în sistem a fost atenuat treptat, și se revine la starea sa inițială. Prin urmare, oscilațiile naturale sunt întotdeauna amortizată.
Prin natura lor, variații pot fi mecanice, electromagnetice, electromecanice, etc. fluctuațiile pot apărea într-un circuit care conține inductanțe și capacități. Acest circuit se numește circuit de oscilație.
Înțelege procesele care au loc în circuitul rezonant, va Fig. 9.2.

Fig. 9.3 ilustrează un circuit oscilant cu o conexiune paralelă de inductanță și capacitate. Rezistența este luată în considerare faptul că, în orice circuit real, are o pierdere de energie, precum și din motive de simplitate, vom presupune că ele apar numai în această rezistență. Excitația vibrațiilor în circuit se realizează prin furnizarea unei scurte impulsuri de tensiune de durată egală osciloscop timp fasciculului retrace.

Având în vedere că. și împărțirea ambelor părți de. Obținem o ecuație diferențială de oscilație amortizată:
Soluția ecuației (9.2) cu <имеет вид:
în care - taxa pe condensator la un moment dat. - coeficientul de amortizare; - frecvența ciclică oscilație amortizată.
Pentru Amortizare mici, de exemplu, la <<:
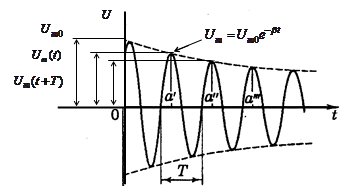
În conformitate cu (9.3), tensiunea condensatorului va varia conform legii:
Energie. stocate în circuitul în timpul duratei impulsului scade exponențial:
.
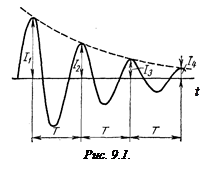
vibrații amortizarii acest caz, este, de obicei, caracterizat printr-un decrement logaritmic de oscilații. egal cu logaritmul raportului dintre amplitudinile a două oscilații succesive (Figura 9.4.):
La atenuare scăzută:
De multe ori, în loc de decrementare logaritmică pentru caracteristicile de circuit, un factor de calitate:
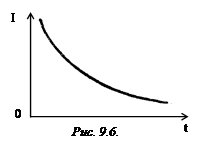
Pentru atenuarea mare, astfel încât >>. în loc de oscilații aperiodice au loc de descărcare a condensatorului (Fig. 9.6).