Simetria în ceea ce privește punctul
Fie G - punct fix și X - punct aleatoriu în planul (a se vedea figura 187.). Am amâna extinderea OX segment al punctului OX O segment“, egal cu OX.
Punctul X „este numit un punct X simetric în raport cu punctul A. punct simetric punctul O este foarte punctul O. Este evident că un punct simetric la punctul X“, este un punct X.
Cifrele de conversie în figura F F „în care fiecare punct X devine un punct X“, care este simetrică în raport cu un punct dat O se numește o transformare de simetrie în raport cu punctul O. În acest caz, F și F „cifra a spus să fie simetrice în raport cu punctul O (fig. 188).
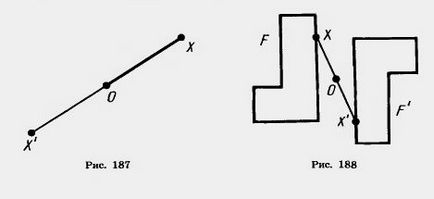
Dacă transformarea simetrie în raport cu punctul O ia forma F o, ea nazyvaetsyatsentralno simetrică. și punctul G este centrul de simetrie.
De exemplu, un paralelogram este central figura simetrică. Centrul său de simetrie este punctul de intersecție al diagonalelor (Fig. 189).
Teorema 9.2. Transformare punct simetrie în raport cu o mișcare.
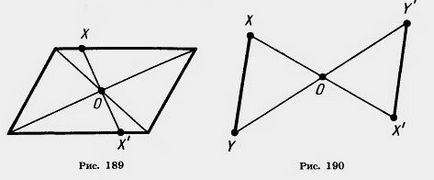
Dovada. Fie X și Y - două puncte arbitrare ale figura F (190 Fig.). simetrie de conversie cu privire la punctul O le transferă la punctele X „și Y.
Luați în considerare triunghiuri XOY și X'OY“. Aceste triunghiuri sunt egale, pe baza egalității primul triunghi. Acestea au inclus unghiuri sunt pe cale atât pe verticală și OX = OX „OY = OY“, prin definiție, simetrie în jurul punctului O. Din egalitatea triunghiurilor ar trebui să fie egalitatea armelor: XY = x'y“. Aceasta înseamnă că simetria în ceea ce privește punctul O este mișcare. Acest lucru dovedește teorema.
A. V. Pogorelov, Geometrie pentru clasele 7-11, manual pentru instituțiile de învățământ