Tema: „Ecuația irațională a formei. . "
ecuații Irrational sunt ecuații în care variabila se găsește sub semnul rădăcinii (radical) sau semna ridicarea la o putere fracționată.
Ecuația forma f (x) = g (x), în cazul în care cel puțin una dintre expresiile f (x) sau g (x) este ecuație irațional irațional.
Proprietățile de bază ale radicalilor:
- Toți radicalii chiar și gradul sunt aritmetice, adică în cazul în care radicand este negativ, atunci radicalul nu are nici un sens (nu există); dacă radicand este zero, radicalul de asemenea, egal cu zero; în cazul în care radicand este pozitiv, atunci există o valoare radicală și pozitivă.
- Toți radicalii grad nui determinat pentru orice valoare a radicand. În acest caz, radicalul este negativ în cazul în care radicand este negativ; este zero dacă radicand este zero; pozitiv în cazul în care cuceriți este pozitiv.
Metode de rezolvare a ecuațiilor iraționale
Rezolva ecuație irațională - înseamnă a găsi toate valoare variabilă validă, care atunci când este substituit în ecuația originală, ea devine o adevărată egalitate numerică, sau pentru a dovedi că aceste valori nu există. ecuații irationale sunt rezolvate pentru setul de numere reale R.
Intervalul de toleranță al ecuației constă în acele valori ale variabilei în care toate expresie non-negativ sub semnul radical chiar grad.
Principalele metode de rezolvare a ecuațiilor iraționale sunt:
a) metoda de construcție a ambelor părți ale ecuației în același grad;
b) o metodă de introducere a unor noi variabile (modificări metodei);
c) Workarounds rezolvarea ecuațiilor iraționale.
Acest articol se va concentra pe examinarea ecuațiile de mai sus un anumit tip și vom da 6 metode de rezolvare a unor astfel de ecuații.
Această metodă necesită înmulțire și formule prescurtate nu conțin pietre „subacvatice“, adică Aceasta nu duce la apariția unor rădăcini străine.
Am rescrie ecuația în formă de cub și vozvedom ambele părți. Obținem o ecuație echivalentă cu ecuația dată,
Exemplul 2: rezolva ecuația.
Am rescrie ecuația în formă de cub și vozvedom ambele părți. Obținem o ecuație echivalentă cu ecuația dată
și ia în considerare ecuația obținută ca o rădăcină pătrată a unei rude
prin urmare, discriminante este 0, iar ecuația poate avea o soluție x = -2.
Notă. Verificarea poate fi omisă în cazul doreshivaetsya ecuația de gradul doi.
2 metodă. formula cubed.
Va continua să construiască ecuația într-un cub, dar utilizarea unor formule modificate de multiplicare prescurtate.
(Modificarea ușoară a formulelor cunoscute), atunci
Exemplul 3. Rezolva ecuația.
Vozvedom ecuație cubică folosind formulele indicate mai sus.
Cu toate acestea, expresia trebuie să fie egală cu partea dreaptă. Prin urmare, avem:
Acum, cu tocati obținem ecuația de gradul doi de obicei:
, și doi dintre rădăcinile sale
Ambele valori, așa cum se arată prin cec, corectă.
Dar face tot conversia este echivalent? Înainte de a răspunde la această întrebare, să rezolve o altă ecuație.
Exemplul 4.. Rezolva ecuația.
Creșterea, ca și mai înainte, ambele părți ale treilea grad, avem:
Locație (având în vedere că expresia în paranteze este aceeași), obținem:
. Obținem și să verifice .Sdelaem de x = 0 -postoronny rădăcină.
Răspunsuri la întrebarea: „De ce există o rădăcini străine?“
Egalitatea presupune egalitate. Înlocuiți cu c, obținem:
Este ușor de a verifica identitatea
Deci, în cazul în care una sau. Ecuația poate fi scrisă sub forma.
Înlocuirea cu c, vom vedea că în cazul în care, fie, sau
Prin urmare, atunci când se utilizează această metodă de soluție trebuie neapărat să facă o verificare de fond și asigurați-vă că nu rădăcini străine.
3 metode. Metoda sistemului.
Exemplul 5. Solve ecuație.
Introducem o înlocuire, compoziție, și de a rezolva un sistem de ecuații.
în cazul în care este evident că
A doua ecuație se obține, astfel încât o combinație liniară de expresii din radicalii nu depinde de variabila originală.
Este ușor de făcut. că sistemul nu are soluții, și, prin urmare ecuația originală nu are nici o soluție.
Răspuns. Nu există rădăcini.
Exemplul 6. Solve ecuație.
Introducem o înlocuire, compoziție, și de a rezolva un sistem de ecuații.
Revenind la variabila originală, avem:
4 metode. Folosind o funcție monotonă.
Înainte de a putea utiliza această metodă pentru a transforma teoria.
Avem nevoie de următoarele proprietăți:
- Dacă funcția y = f (x) și y = g (x) crește (descrește) într-un set, atunci funcția y = f (x) + g (x), de asemenea, crește (scade) în acest set.
- Dacă funcția y = f (x) și y = g (x) crește (descrește) într-un set, la care ambele iau valori nenegative pentru toate x admisibile, funcția y = f (x) g (x) crește (scade ) pentru un set dat.
- Dacă funcția y = f (x) un monotone, ecuația f (x) = a nu are mai mult de o soluție.
- Dacă funcția y = f (x) și y = g (x) au diferit monotonie caracter, ecuația f (x) = g (x) nu are nici o soluție mai mult de unul.
- tip de funcție crește cu k> 0 și scade pentru k<0.
Exemplul 7. rezolva ecuația.
Partea stângă a ecuației o funcție crescătoare, iar dreapta - numărul, și anume, constant, prin urmare, ecuația are cel mult o rădăcină care va selecta: x = 9. Asigurați-vă că root este potrivit.
Exemplul 8. Solve ecuație.
Partea stângă a ecuației o funcție crescătoare, iar dreapta - numărul, și anume, constant, prin urmare, ecuația are cel mult o rădăcină care va selecta: x = -2. Asigurați-vă că root este potrivit.
Această din urmă ecuație poate fi reprezentat de o altă formă, apoi partea dreaptă a ecuației scade, în timp ce crește stânga, deci ecuația are cel mult o rădăcină. și să ajungă la x = -2.
5 metode. Metoda grafică pentru rezolvarea ecuațiilor.
Exemplul 9. rezolva ecuația
Rescriem ecuația ca: alcatuim grafice ale părților stânga și dreapta.
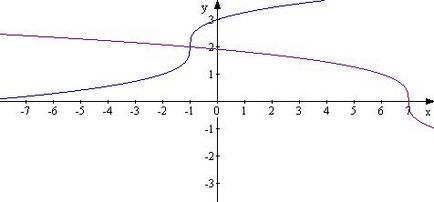
Graficele se intersectează în punctul (1, 2), x = -1.
Verificați: 2 = 2 (dreapta).
x = - 1 este rădăcina ecuației inițiale.
6 metodă. metoda de substituție
Exemplu. Rezolva ecuația:
Introducem un înlocuitor. Să atunci ecuația devine
t = 0, sau - nu există soluții.
t = 0, revenind apoi la variabila originală, avem: x = -8.
Sarcini pentru decizia independentă.