Dacă curba este dată de ecuațiile parametrice
,
Acea suprafață este formată prin rotație în jurul axei arcului acestei curbe se calculează cu formula:
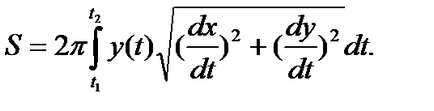
în cazul în care valoarea parametrului corespunzător capetele arcului.
Dacă curba este dată de ecuațiile
,
În loc să obținem formula
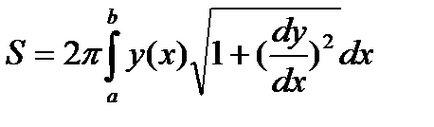
În cazul în care - abscise începutul și sfârșitul arcului.
6.5.1.Nayti suprafață formată în jurul axei de rotație a arcului de o sinusoidă la
Decizie. Găsim apoi
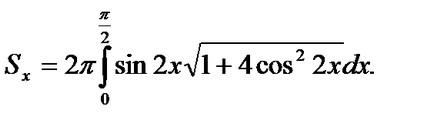
Noi facem schimbarea de variabilă
Găsiți limitele de integrare pentru:
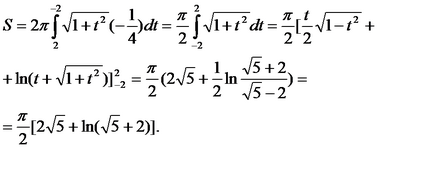
suprafață suprafață 6.5.2.Nayti formată prin rotirea în jurul axei Ox a arcului parabolei cubi încheiat între directe și
Decizie. Prin construirea unui arc de parabole între punctele A și B în cazul în care,
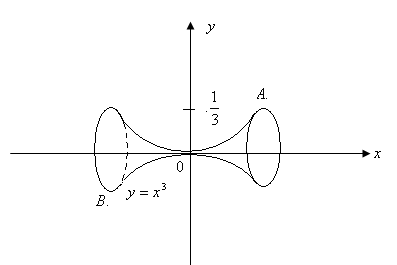
Menționăm că suprafața formată prin rotirea arcului în jurul axei Ox este format din două părți identice.
Prin urmare, conform formulei avem
Pentru a calcula cred integralei
suprafață 6.5.3.Nayti formată prin rotirea în jurul axei orizontale astroidă
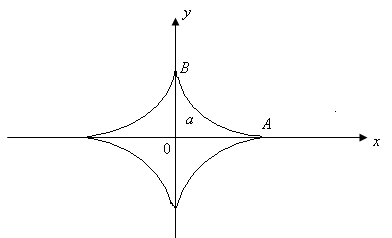
Forma integrands în conformitate cu formula
Parametrul schimbare e de la t = 0 corespunde punctului asupra mișcării astroidă de la A la B. Arcul AB cu rotirea axei Ox jumătate din suprafața dorită, așa
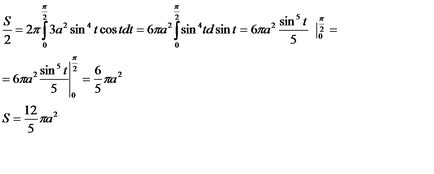
Cererile de integralele definite pentru a rezolva probleme de fizică.